この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
位置演算子の固有関数の運動量表示
こんにちは,クロメルです. S1Sz0の状態に関する考察 に続き,
今度は位置演算子 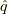 と運動量演算子
と運動量演算子 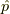 の固有状態の変換を書きます.
の固有状態の変換を書きます.
基本事項
これからしたいことは,位置演算子 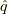 の固有関数
の固有関数 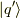 を
運動量演算子
を
運動量演算子 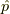 の固有関数
の固有関数 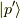 で表す [*] ことです.
で表す [*] ことです.
| [*] | : ディラックの書き方に習い,プライム  は,特定の実数を表すことにします. は,特定の実数を表すことにします. 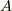 の演算子は,ハット の演算子は,ハット 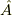 をつけて表します. をつけて表します. |
位置演算子 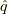 の固有関数は,
の固有関数は,

を満たし, 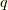 表示をすると,
表示をすると,

となります.
また,運動量演算子 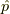 の固有関数は,
の固有関数は,

を満たし, 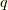 表示をすると,
表示をすると,

また,恒等演算子,

を使います.
ここまでに挙げた基本的な事項は,参考文献に挙げた「量子力学」ディラック著などを参照してください.
本題
さて,いよいよ展開してみましょう.
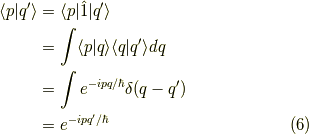
これは,位置 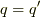 に局在する粒子は,
運動量
に局在する粒子は,
運動量 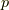 が定まらないと言うハイゼンベルクの不確定性原理
を表しています.
実空間と運動量空間は,フーリエ変換で結ばれています.
が定まらないと言うハイゼンベルクの不確定性原理
を表しています.
実空間と運動量空間は,フーリエ変換で結ばれています.
今日はここまで.