この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
留数定理とは
この記事では,留数定理をかなり大雑把に,使い道まで解説します.
基本
留数定理は,複素線積分に関する定理です. もし,複素線積分が正則な領域を囲むなら, 積分値はゼロになります.これがコーシーの積分定理です.
ところが,囲む領域の中に正則でない点,例えば 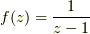 のように,
非正則点(これを特異点と言います)があると,一周しても積分値がゼロでないことがあります.
だから,何なんだ.と思うでしょうが,これが非常に役に立ちます.
後で説明しますので,お楽しみに.
のように,
非正則点(これを特異点と言います)があると,一周しても積分値がゼロでないことがあります.
だから,何なんだ.と思うでしょうが,これが非常に役に立ちます.
後で説明しますので,お楽しみに.
発想
次の積分を計算しましょう.  を
を 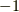 でない整数とします.
でない整数とします. 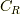 は原点を囲む半径
は原点を囲む半径 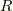 の円です.
の円です. 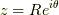 とすると,
とすると, 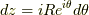 で積分範囲は,
で積分範囲は, 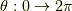 です.
です.
![\int_{C_R} z^n dz &= \int_0^{2 \pi} \left( R^n e^{i n \theta} \right) i R e^{i \theta} d \theta \\&= i \int_0^{2 \pi} R^{n+1} e^{i (n+1) \theta} d \theta \\&= \left[ \dfrac{i}{i(n+1)} R^{n+1} e^{i (n+1) \theta} \right]_0^{2\pi} \\&= \dfrac{1}{(n+1)} R^{n+1} e^{i2 (n+1) \pi} - \dfrac{1}{(n+1)} R^{n+1} e^{0} \\&= 0\tag{1}](http://hooktail.maxwell.jp/kagi/6ee08b583161e6ff8ac6bff530465dd2.png)
ですね.では,これ見よがしに 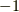 を除外しましたが,この時どうなるか.
次に示します.
を除外しましたが,この時どうなるか.
次に示します.
![\int_{C_R} z^n dz &= \int_0^{2 \pi} \left( R^{-1} e^{- i \theta} \right) i R e^{i \theta} d \theta \\&= i \int_0^{2 \pi} 1 d \theta \\&= i \left[ \theta \right]_0^{2\pi} \\&= 2 \pi i\tag{2}](http://hooktail.maxwell.jp/kagi/9eeda7c674d5c17cc50fa0db11a9976e.png)
これだけ残るのです.しかもこの積分は示しませんが,積分路がこの点  を囲ってさえいれば,いつでも
を囲ってさえいれば,いつでも 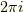 となります.
となります.
ローラン展開
ここで,  をテイラー展開で
をテイラー展開で 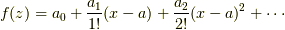 と展開できますよね.
でも,これは
と展開できますよね.
でも,これは  の様な関数は展開できません.(この辺はどういう関数ならテイラー展開で良いかはよく知りません.)そこで,テイラー展開の拡張でローラン展開と言うものがあります.例えば,
の様な関数は展開できません.(この辺はどういう関数ならテイラー展開で良いかはよく知りません.)そこで,テイラー展開の拡張でローラン展開と言うものがあります.例えば,
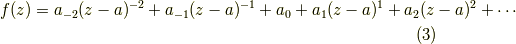
があげられます.テイラー展開では 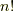 で割っていましたが,ローラン展開ではしませんね.ここで冪数の最低次の数を極の次数といい,この場合は,2次の極と言います.大抵は 1次の極の計算を知っていれば対処できます.もし,この次数が無限なら,真性特異点と言います.では,この式
で割っていましたが,ローラン展開ではしませんね.ここで冪数の最低次の数を極の次数といい,この場合は,2次の極と言います.大抵は 1次の極の計算を知っていれば対処できます.もし,この次数が無限なら,真性特異点と言います.では,この式 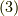 を囲った複素線積分(積分路
を囲った複素線積分(積分路 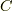 )はどうなるでしょう.
)はどうなるでしょう. 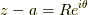 とすれば,これも
とすれば,これも  の寄与のみが残り,
の寄与のみが残り,
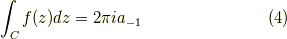
となるのです.
いよいよ留数の登場
実は,式 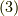 の
の 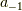 はわざわざ積分しなくても求まります.
式
はわざわざ積分しなくても求まります.
式 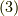 に
に  をかけてみましょう.
をかけてみましょう.
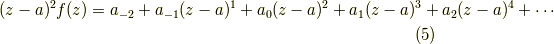
さらに,  で微分してみましょう.
で微分してみましょう.
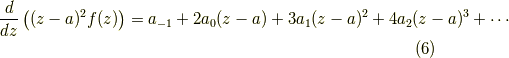
そして,  を代入すると,
を代入すると,
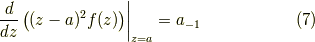
となります.この上式の左辺が留数と呼ばれるものです.

と書きます.
一次の極なら話はもっと簡単で,
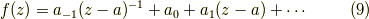
なのですから,
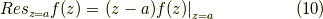
となります.どうです?積分がただの掛け算と代入だけで求まってしまいます.
式 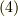 と比べて,
と比べて,

が言えます.これは覚えるべき公式です. もし,他の極も囲った中にあるなら,
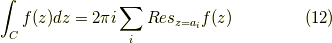
とすればよいです.これを留数定理と呼びます.
使い道
例えば,この積分値が分かるようになると,普通は不定積分が計算できないのに,実関数  の積分
の積分 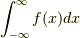 などの定積分が分かるようになります.必ずしも実関数でなくてもよいです.
などの定積分が分かるようになります.必ずしも実関数でなくてもよいです.
具体例を挙げてみます.  として,
として,

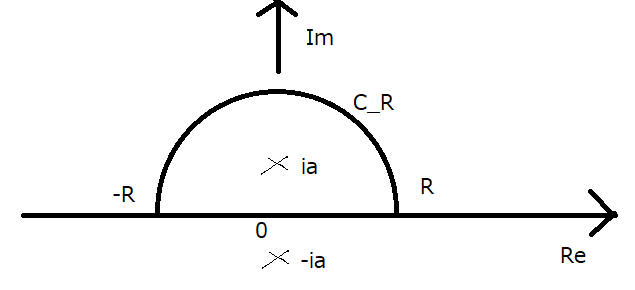
を計算します.それには積分路を図の様に取ります.
この経路  の反時計回り一周分の積分をします.
の反時計回り一周分の積分をします.
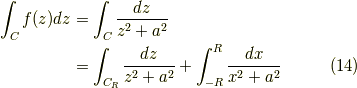
ここで,円弧 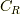 の積分は
の積分は 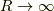 で消えてしまいます.
この辺は詳しく書きません.(cf.フーリエ変換の応用にはジョルダンの補題が役に立ちます)残るのが,
で消えてしまいます.
この辺は詳しく書きません.(cf.フーリエ変換の応用にはジョルダンの補題が役に立ちます)残るのが,

ですね.この 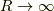 の極限を計算します.
しかし,我々はこの積分一周の値を留数定理から知っているのです.
図に示した通り,極は
の極限を計算します.
しかし,我々はこの積分一周の値を留数定理から知っているのです.
図に示した通り,極は 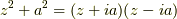 より,
このかまぼこ型の領域には
より,
このかまぼこ型の領域には 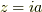 が含まれています.
が含まれています.
![\int_{C} \dfrac{dz}{z^2+a^2} &= 2 \pi i Res_{z = ia} f(z) \\&= 2 \pi i \left[ (z-ia)\dfrac{1}{(z-ia)(z+ia)} \right]_{z=ia} \\&= 2 \pi i \left[ \dfrac{1}{z+ia} \right]_{z=ia} \\&= 2 \pi i \dfrac{1}{2ia} \\&= \dfrac{\pi}{a}\tag{16}](http://hooktail.maxwell.jp/kagi/fe8c60b43ff3e6687a5ed1e539d29a9d.png)
これが言えたので,
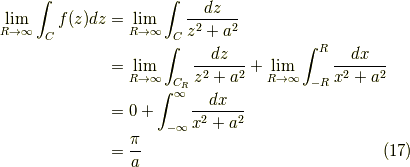
ややこしいですが,つまりは,
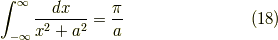
となります. この留数定理は,フーリエ変換やグリーン関数を求める際,強力な道具となります.
今日はここまで,お疲れさまでした.