この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ε-δ論法
ここでは,解析学などでよく目にする 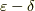 論法というものについて紹介します.この
論法というものについて紹介します.この 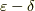 論法は関数の連続性や収束などを示すためによく使われる論法です.紹介記事や練習問題から,ここで何を議論したいのかや特徴などを確認して下さい.
論法は関数の連続性や収束などを示すためによく使われる論法です.紹介記事や練習問題から,ここで何を議論したいのかや特徴などを確認して下さい.
ε-δ論法とは?
まずは,定義を確認します. 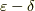 論法とは距離が定義されている空間(距離空間)において,関数の連続性や点列の収束を定義する論法のことです.具体的には,以下のように表記されることが多いです.
論法とは距離が定義されている空間(距離空間)において,関数の連続性や点列の収束を定義する論法のことです.具体的には,以下のように表記されることが多いです.
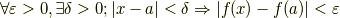
この式の意味はこうです.「任意の有限の正数  に対して,適当な正数
に対して,適当な正数  が存在していて,この
が存在していて,この  が
が 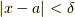 ならば
ならば 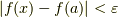 となる.」なお,ここでは
となる.」なお,ここでは  は
は  と
と  の距離のことです. [*]
の距離のことです. [*]
また,上の式はそのまま  に対する関数
に対する関数 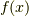 の連続性を定義したものとなっています.これが点列
の連続性を定義したものとなっています.これが点列 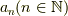 の収束の定義では,
の収束の定義では,
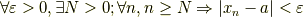
といった形式になります.今度は  の代わりに
の代わりに 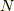 が登場しました.このような形式の論法のときは
が登場しました.このような形式の論法のときは  論法といいます [†] .しかし,これはあくまで形式のお話です.この論法の心は上に書いてある日本語の意味なのです.
論法といいます [†] .しかし,これはあくまで形式のお話です.この論法の心は上に書いてある日本語の意味なのです.
| [*] | 距離という言葉を簡単に使っていますが,実は距離というものは数学の世界では当たり前のものではありません.ここでは,距離がすでに導入されている空間の中で議論をしているので,ヒョイヒョイと話を進めていっています.ここではそれでいいのです.でも,厳密には距離や順序を導入する際,ノルムや順序構造なるもののことを考えてあげなければいけません(普通は自然と順序や距離というものに慣れてしまっているので,それについていちいち考えたりしません).ノルムや順序構造といった概念の存在は,位相(topology)を勉強していく上では,心に留めておくべき存在です.なぜなら,位相の勉強をするときには,私たちが当たり前だと思っている距離や順序といった概念が存在しない空間で近似に関する議論をしていくからです.「距離や順序の概念が存在している空間」と「存在していない空間」.このことに気をつけながら,位相構造がいかなる構造を基礎として成立しているかに迫っていってください. |
| [†] | これに似た形でコーシー列の定義もあります.コーシー列の定義では,「 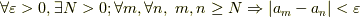 」となっています.違いが分かりますか?詳しくは コーシー列と完備の概念 をご覧下さい. 」となっています.違いが分かりますか?詳しくは コーシー列と完備の概念 をご覧下さい. |
おまけ
上で, 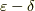 論法について二つの表記を見ました.関数についてと,数列についてです.しかし,この二つは結局同じことを意味しているのです.それは一体どういうことなのか,見てみましょう.まず,数列の収束に関して
論法について二つの表記を見ました.関数についてと,数列についてです.しかし,この二つは結局同じことを意味しているのです.それは一体どういうことなのか,見てみましょう.まず,数列の収束に関して
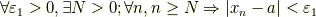
という表現がありました.これに対し,
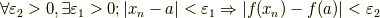
という表現が成り立つように,  を決めてやれば,結局上の式と下の式は同じことを言っていることになります.つまり,
を決めてやれば,結局上の式と下の式は同じことを言っていることになります.つまり,
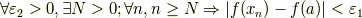
と書き直すことができます.
ε-δ論法の特徴
ここまで,定義の形式を見て,「関数の収束を示すだけならば,もっと他の論法もあるんじゃないのか??」と思われた方,その通りです.関数に限らず写像の収束等を大学で習う場合に,多くの教科書にまず書いてあるのは極限を使ったものです. 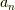 に対して
に対して 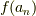 が収束しそうだということを言う場合には,「
が収束しそうだということを言う場合には,「  を無限大にどんどん大きくすれば,
を無限大にどんどん大きくすれば, 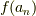 は定数
は定数  にどんどん近づく」という意味で,
にどんどん近づく」という意味で,

という具合に表現します.いったい,これらの違いは何なのでしょうか?
まずは極限を使っているかいないかという点です. 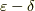 論法では極限ではなく有限の値(
論法では極限ではなく有限の値( 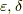 )を使い,その有限の値中の近傍に変数や関数値が含まれているかどうかが問題になります.つまり,
)を使い,その有限の値中の近傍に変数や関数値が含まれているかどうかが問題になります.つまり, 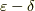 論法は近傍の極限を考える過程の段階なのです.
論法は近傍の極限を考える過程の段階なのです.
位相へ一歩踏み出す
また,今の議論から 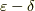 論法は集合を使って定式化することも可能だと分かります.ここで,
論法は集合を使って定式化することも可能だと分かります.ここで, 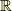 における中心
における中心  ,半径
,半径  の開球 [‡] を
の開球 [‡] を 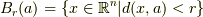 とすると,
とすると,
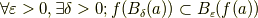
と定式化できます.この開球は  の近傍を表し,
の近傍を表し,  の近傍空間のことを距離や順序を使わず,集合論のみで議論できることを示唆しています
の近傍空間のことを距離や順序を使わず,集合論のみで議論できることを示唆しています
Important
開球を使えば, 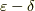 論法を使わなくても近傍の概念を持ち込める.
論法を使わなくても近傍の概念を持ち込める.
上の場合はまだ距離空間での議論ではありますが,すでに集合論での議論は可能ですね.最も明白な例を挙げると,連続写像  の
の 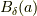 に対する像は
に対する像は 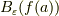 である…といった具合です.これを距離空間で考えずに,開球や開集合だけが定義された空間で議論するのが 位相 なのです.
である…といった具合です.これを距離空間で考えずに,開球や開集合だけが定義された空間で議論するのが 位相 なのです.
| [‡] | 開球とは,  次元空間における境界線のない球のことを言います.1次元なら開区間 次元空間における境界線のない球のことを言います.1次元なら開区間 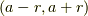 ,2次元なら淵のない円盤,3次元なら表面(境界)のない中身がつまった球のことです. ,2次元なら淵のない円盤,3次元なら表面(境界)のない中身がつまった球のことです. |
練習問題
写像 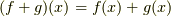 が点
が点 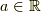 で連続であることを示せ.ただし,写像
で連続であることを示せ.ただし,写像  は点
は点 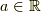 で連続であるとする.
で連続であるとする.
proof
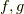 がそれぞれ連続であるから
がそれぞれ連続であるから  ,
, 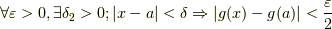 が成り立っている.ここで,
が成り立っている.ここで, 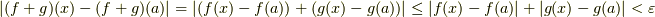 となるから,
となるから, 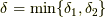 とすると,以下のことが成り立つ.
とすると,以下のことが成り立つ. 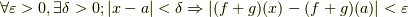 .したがって,
.したがって, 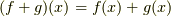 は連続である.
は連続である.
| [§] | ここで,  は任意に選んでいいので,ここでは最後にきれいな形になるように, は任意に選んでいいので,ここでは最後にきれいな形になるように, 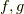 の連続の定義となる の連続の定義となる  を を 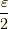 として用いました. として用いました. |