この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ヒルベルト変換とフーリエ変換
(書体に関するバグがありまして, 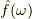 と
と 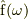 は同じものです.)
ヒルベルト変換
は同じものです.)
ヒルベルト変換 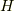 とは,主値積分を
とは,主値積分を 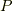 とした時,その関数
とした時,その関数 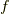 への作用を,
への作用を,
![H[f(t)] = \dfrac{1}{\pi} P \int_{-\infty}^{\infty} \dfrac{f(t^\prime)}{t-t^\prime}dt^\prime \tag{1}](http://hooktail.maxwell.jp/kagi/241b940185c69b11645569b31d0bcc41.png)
というものです.これは符号関数
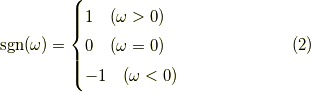
と関数 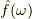 (f(t)のフーリエ変換)の積
(f(t)のフーリエ変換)の積 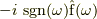 のフーリエ逆変換から自然に出てきます.
のフーリエ逆変換から自然に出てきます.
この記事では,
![\mathcal{F}^{-1}[-i \ \rm{sgn}(\omega) \hat{f}(\omega)] &= H[f(t)] \\\mathcal{F}\left[ H[f(t)] \right] &= -i \ \rm{sgn}(\omega) \hat{f}(\omega)](http://hooktail.maxwell.jp/kagi/7229da0291a0bd8fcf514c847aae91bc.png)
を示します.
結果がヒルベルト変換になる逆フーリエ変換
実際,逆フーリエ変換を施してみましょう.以下では 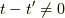 とします.(
とします.( 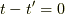 の時ω積分は発散します)
の時ω積分は発散します)
![\mathcal{F}^{-1}[-i \ \rm{sgn}(\omega) \hat{f}(\omega)]&= \int_{-\infty}^\infty \dfrac{d \omega}{2 \pi} \left( -i \ \rm{sgn}(\omega) \hat{f}(\omega) e^{i \omega t} \right) \\&= \dfrac{1}{2 \pi i} \int_{-\infty}^\infty d \omega \ \rm{sgn}(\omega) e^{i \omega t} \left( P \int_{-\infty}^\infty d t^\prime f(t^\prime) e^{-i \omega t^\prime} \right) \\&= \dfrac{1}{2 \pi i} P \int_{-\infty}^\infty d t^\prime f(t^\prime) \left( \int_{-\infty}^\infty d \omega \ \rm{sgn}(\omega) e^{i \omega (t-t^\prime)} \right) \\&= \dfrac{1}{2 \pi i} P \int_{-\infty}^\infty d t^\prime f(t^\prime) \left( \int_0^\infty d \omega e^{i \omega (t-t^\prime)} - \int_{-\infty}^0 d \omega e^{i \omega (t-t^\prime)} \right) \\&= \dfrac{1}{2 \pi i} P \int_{-\infty}^\infty d t^\prime f(t^\prime) \left( \left[ \dfrac{e^{i \omega (t-t^\prime)}}{i(t-t^\prime)} \right]_0^{\infty} - \left[ \dfrac{e^{i \omega (t-t^\prime)}}{i(t-t^\prime)} \right]_{-\infty}^0 \right) \\&= \dfrac{1}{2 \pi i} P \int_{-\infty}^\infty d t^\prime f(t^\prime) \left( \dfrac{-2}{i(t-t^\prime)} \right) \\&= \dfrac{1}{\pi} P \int_{-\infty}^\infty d t^\prime \dfrac{f(t^\prime)}{t-t^\prime} \\&= H[f(t)] \tag{3}](http://hooktail.maxwell.jp/kagi/bcc8f0d49599b80f67f49a65fd5c8832.png)
と,この様にヒルベルト変換が出てきました.
ヒルベルト変換のフーリエ変換
式 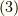 をフーリエ変換してみます.(主値積分とは積分記号に付くものではなく
をフーリエ変換してみます.(主値積分とは積分記号に付くものではなく 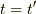 の時を除くと考えれば良さそうです.)
の時を除くと考えれば良さそうです.)
![\mathcal{F}\left[ H[f(t)] \right] &= \int_{-\infty}^\infty dt e^{-i \omega t} \dfrac{1}{\pi} P \int_{-\infty}^\infty d t^\prime \dfrac{f(t^\prime)}{t-t^\prime} \\&= \dfrac{1}{\pi} \int_{-\infty}^\infty d t^\prime e^{-i \omega t^\prime} f(t^\prime) \left( P \int_{-\infty}^\infty dt \dfrac{e^{-i \omega (t-t^\prime)}}{t-t^\prime} \right)\tag{4}](http://hooktail.maxwell.jp/kagi/8319eeb40aa2a8775a2d778aa8cdcb01.png)
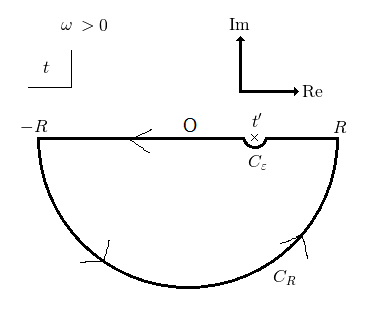
式 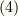 の最終行の丸かっこ内の
の最終行の丸かっこ内の 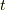 積分を実行します.被積分関数を
積分を実行します.被積分関数を 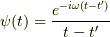 と置くと,
と置くと, 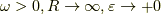 の時,下半面で
の時,下半面で 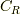 積分はゼロになり(ジョルダンの補題),
積分はゼロになり(ジョルダンの補題), 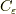 は
は 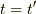 で時計回りに半周に対し,留数
で時計回りに半周に対し,留数 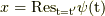 が反時計回りで一周なので,
が反時計回りで一周なので, 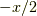 となります.(この証明は,下記参考文献のp.105にあります.)後は実軸上の直線部分が求めたい積分のマイナス一倍となります.この領域には極が含まれていないので,積分は一周してゼロです.つまり,
となります.(この証明は,下記参考文献のp.105にあります.)後は実軸上の直線部分が求めたい積分のマイナス一倍となります.この領域には極が含まれていないので,積分は一周してゼロです.つまり,
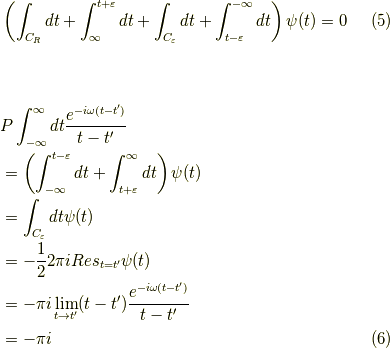
これと同様に 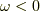 の時の積分を行うと,
の時の積分を行うと, 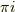 が得られます.
が得られます.
よって,

と分かります.( 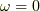 の時はどうしたものか?)
よって,式
の時はどうしたものか?)
よって,式 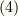 の計算を続行すると,
の計算を続行すると,
![\mathcal{F}\left[ H[f(t)] \right] &= \dfrac{1}{\pi} \int_{-\infty}^\infty d t^\prime e^{-i \omega t^\prime} f(t^\prime) \left( P \int_{-\infty}^\infty dt \dfrac{e^{-i \omega (t-t^\prime)}}{t-t^\prime} \right) \\&= \dfrac{1}{\pi} \int_{-\infty}^\infty d t^\prime e^{-i \omega t^\prime} f(t^\prime) \left( -\pi i \ \rm{sgn}(\omega) \right) \\&= -i \ \rm{sgn}(\omega) P \int_{-\infty}^\infty d t^\prime e^{-i \omega t^\prime} f(t^\prime) \\&= -i \ \rm{sgn}(\omega) \hat{f}(\omega)\tag{8}](http://hooktail.maxwell.jp/kagi/2db8c9799cd8eeef4908f50e4e9ec7d1.png)
となり,無事ヒルベルト変換のフーリエ変換が求まりました.
今日はここまで,お疲れさまでした!