この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
双対基底

座標変換のされ方に従い，共変ベクトルと反変ベクトルという種類があることを 共変ベクトルと反変ベクトル で勉強しました．また，通常は基底ベクトルと成分で添字の上下が逆になるように表現します．つまり，共変ベクトルでは成分の添字は右下に，基底の添字は右上に書き，反変ベクトルでは成分の添字は右上に，基底の添字は右下に書きます．

この記事では，ここに出てきた，共変基底と反変基底という二種類の基底の相互関係を勉強します．

双対基底

二つの基底の組 \{ \bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} , \ \{ \bm{e^{1}},\bm{e^{2}},\bm{e^{3}} \} が次の関係を満たすとき，この二つの基底は互いに 双対である と言い，これらを 双対基底 もしくは 相反基底 と呼びます．

\bm{e_{i}} \cdot \bm{e^{j}} = {\delta}_{i}^{j} \tag{1}

既に 共変ベクトルと反変ベクトル の記事に双対基底は出てきていましたが，互いの関係には何ら触れられていませんでした．いよいよ話題は，双対基底が互いに満たす関係へと突入です．

Important

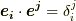
\bm{e_{i}} \cdot \bm{e^{j}} = {\delta}_{i}^{j}

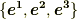双対基底の定義式はこれだけです．この次のセクションでは，実際に基底 \{ \bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} が与えられたときに，その双対基底 \{ \bm{e^{1}},\bm{e^{2}},\bm{e^{3}} \} をどのように決められるのかを考えます．

双対基底を求める

まず定義より 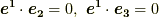\bm{e^{1}}\cdot \bm{e_{2}}=0, \ \bm{e^{1}}\cdot \bm{e_{3}}=0 が成り立ちますから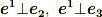， \bm{e^{1}} \bot \bm{e_{2}}, \ \bm{e^{1}} \bot \bm{e_{3}} が分かります．これより 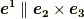\bm{e^{1}} \parallel \bm{e_{2}} \times \bm{e_{3}} が言えますから，適当なスカラー \lambda を使って次式のように表現できます．

\bm{e^{1}}=\lambda (\bm{e_{2}}\times \bm{e_{3}}) \tag{2}

一方，やはり定義より 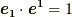\bm{e_{1}} \cdot \bm{e^{1}}=1 ですから，式 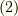(2) の両辺に \bm{e_{1}} の内積を取ると次式が成り立つはずです．

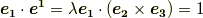
\bm{e_{1}}\cdot \bm{e^{1}}=\lambda \bm{e_{1}}\cdot (\bm{e_{2}}\times \bm{e_{3}})=1

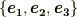これより，先ほど仮に置いておいた定数 \lambda を共変基底 \{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} だけで表現できます．

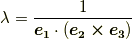
\lambda = \frac{1}{\bm{e_{1}} \cdot (\bm{e_{2} \times \bm{e_{3}}})}

これを式 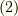(2) に代入すれば次式を得ます．

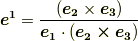
\bm{e^{1}}=\frac{ (\bm{e_{2}}\times \bm{e_{3}}) }{\bm{e_{1}} \cdot (\bm{e_{2} \times \bm{e_{3}}})}

与えられた共変基底 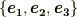\{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} だけで反変基底 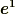\bm{e^{1}} を表現できました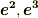． \bm{e^{2}},\bm{e^{3}} も同様に求めることが出来ます．以下に結果だけ書きます．

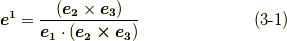
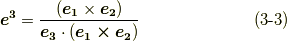
\bm{e^{1}}=\frac{ (\bm{e_{2}}\times \bm{e_{3}}) }{\bm{e_{1}} \cdot (\bm{e_{2} \times \bm{e_{3}}})} \tag{3-1} \bm{e^{2}}=\frac{ (\bm{e_{3}}\times \bm{e_{1}}) }{\bm{e_{2}} \cdot (\bm{e_{3} \times \bm{e_{1}}})} \tag{3-2} \bm{e^{3}}=\frac{ (\bm{e_{1}}\times \bm{e_{2}}) }{\bm{e_{3}} \cdot (\bm{e_{1} \times \bm{e_{2}}})} \tag{3-3}

全く同様の計算により，逆に反変基底 \{\bm{e^{1}},\bm{e^{2}},\bm{e^{3}} \} で共変基底 \{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} を表わすこともできます．

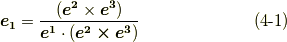
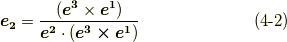
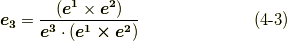
\bm{e_{1}}=\frac{ (\bm{e^{2}}\times \bm{e^{3}}) }{\bm{e^{1}} \cdot (\bm{e^{2} \times \bm{e^{3}}})} \tag{4-1} \bm{e_{2}}=\frac{ (\bm{e^{3}}\times \bm{e^{1}}) }{\bm{e^{2}} \cdot (\bm{e^{3} \times \bm{e^{1}}})} \tag{4-2} \bm{e_{3}}=\frac{ (\bm{e^{1}}\times \bm{e^{2}}) }{\bm{e^{3}} \cdot (\bm{e^{1} \times \bm{e^{2}}})} \tag{4-3}

式 (3-1)(3-2)(3-3)(4-1)(4-2)(4-3) が，確かに式 (1) の定義を満たすことを確認してみてください．

双対基底の性質

双対基底の性質として，次の二つが重要です．

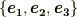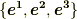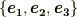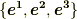  1. もしも \{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} が右手系ならば \{\bm{e^{1}},\bm{e^{2}},\bm{e^{3}} \} も右手系， \{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} が左手系ならば \{\bm{e^{1}},\bm{e^{2}},\bm{e^{3}} \} も左手系になります．逆も然りです．右手系と左手系が入れ替わることはありません．
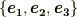  2. もしも \{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} が直交基底ならば，双対基底は 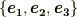\{\bm{e_{1}},\bm{e_{2}},\bm{e_{3}} \} 自身になります．（二つの双対基底は同一になります．）
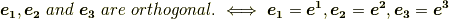
\bm{e_{1}},\bm{e_{2}} \ and \ \bm{e_{3}} \ are \ orthogonal. \ \Longleftrightarrow \ \bm{e_{1}}=\bm{e^{1}},\bm{e_{2}}=\bm{e^{2}}, \bm{e_{3}} =\bm{e^{3}}

この記事では，双対基底が満たすべき関係として 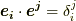\bm{e_{i}} \cdot \bm{e^{j}} = {\delta}_{i}^{j} を定義しました．それ以降の議論は全て双対基底の定義式だけから導かれたものです．計算自体は難しくなかったと思いますが，『そもそも最初の人はどうして双対基底なんて思いついたんだ？』という，いわば双対基底の概念の出所ともいうべく部分がまだ不明瞭だと思います．

双対基底の概念の拠り所ともなっている数学的な背景は，次の ベクトル空間と線形写像 ， 双対空間 で取り上げます．抽象的な議論になりますが，そもそも私達がその上でベクトルの計算を行っている，いわば数学的な土俵に関して議論し，双対基底という概念が出てくる背後の代数的な構造そのものを勉強することになります．

また，基底が直交しない場合，ベクトルの成分を表わすのは面倒ですが，双対基底の概念を使うと簡単に表わすことができます． ベクトルの成分を表わす でその話題を取り上げます．これは双対基底の一つの利用法です．