この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
とある外微分の公式

この記事では，参考文献『理論物理学のための幾何学とトポロジーI』にある有用な公式について説明します． 短い記事です．

公式

公式とは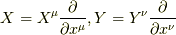， X=X^\mu \dfrac{\partial}{\partial x^\mu},Y=Y^\nu \dfrac{\partial}{\partial x^\nu} をベクトル場とし，一形式 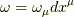\omega=\omega_\mu dx^\mu とします．

d \omega(X,Y) = X[\omega(Y)]-Y[\omega(X)]-\omega([X,Y]) \tag{1}

というものです．参考文献には d \omega([X,Y]) とありますが，これは誤植です．

さらに勘違いしやすい点として，スカラー 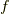f に対して， X[f] = X^\mu(\partial_\mu f) という， X[f] はベクトルのスカラー倍ではなく，スカラーを表しています．

公式の証明

まず，与式の左辺は，

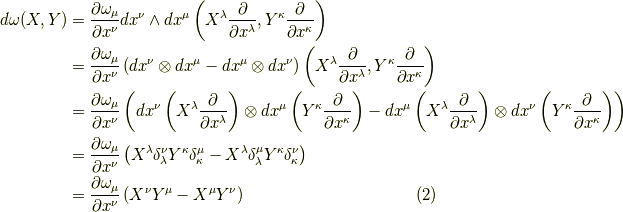
d \omega(X,Y) &= \dfrac{\partial \omega_\mu}{\partial x^\nu} dx^\nu \wedge dx^\mu \left( X^\lambda \dfrac{\partial}{\partial x^\lambda}, Y^\kappa \dfrac{\partial}{\partial x^\kappa} \right) \\&= \dfrac{\partial \omega_\mu}{\partial x^\nu} \left( dx^\nu \otimes dx^\mu - dx^\mu \otimes dx^\nu \right) \left( X^\lambda \dfrac{\partial}{\partial x^\lambda}, Y^\kappa \dfrac{\partial}{\partial x^\kappa} \right) \\&= \dfrac{\partial \omega_\mu}{\partial x^\nu} \left( dx^\nu \left( X^\lambda \dfrac{\partial}{\partial x^\lambda} \right) \otimes dx^\mu \left( Y^\kappa \dfrac{\partial}{\partial x^\kappa} \right) - dx^\mu \left( X^\lambda \dfrac{\partial}{\partial x^\lambda} \right) \otimes dx^\nu \left( Y^\kappa \dfrac{\partial}{\partial x^\kappa} \right) \right) \\&= \dfrac{\partial \omega_\mu}{\partial x^\nu} \left( X^\lambda \delta^\nu_\lambda Y^\kappa \delta^\mu_\kappa - X^\lambda \delta^\mu_\lambda Y^\kappa \delta^\nu_\kappa \right) \\&= \dfrac{\partial \omega_\mu}{\partial x^\nu} \left( X^\nu Y^\mu - X^\mu Y^\nu \right)\tag{2}

となります．

また，与式の右辺は，

X[\omega(Y)]-Y[\omega(X)]-\omega([X,Y]) &= X^\nu \partial_\nu(\omega_\mu Y^\mu) - Y^\nu \partial_\nu(\omega_\mu X^\mu) - \omega_\lambda dx^\lambda \left( X^\nu \partial_\nu Y^\mu - Y^\nu \partial_\nu X^\mu \right) \dfrac{\partial}{\partial x^\mu} \\&= X^\nu (\partial_\nu \omega_\mu) Y^\mu + X^\nu \omega_\mu (\partial_\nu Y^\mu) - Y^\nu (\partial_\nu \omega_\mu) X^\mu - Y^\nu \omega_\mu(\partial_\nu X^\mu) \\&- \omega_\lambda \left( X^\nu \partial_\nu Y^\mu - Y^\nu \partial_\nu X^\mu \right) \delta_\mu^\lambda \\&= X^\nu (\partial_\nu \omega_\mu) Y^\mu + X^\nu \omega_\mu (\partial_\nu Y^\mu) - Y^\nu (\partial_\nu \omega_\mu) X^\mu - Y^\nu \omega_\mu(\partial_\nu X^\mu) \\&- \omega_\mu \left( X^\nu \partial_\nu Y^\mu - Y^\nu \partial_\nu X^\mu \right) \\&= X^\nu \dfrac{\partial \omega_\mu}{\partial x^\nu} Y^\mu - Y^\nu \dfrac{\partial \omega_\mu}{\partial x^\nu} X^\mu \\&= \dfrac{\partial \omega_\mu}{\partial x^\nu} \left( X^\nu Y^\mu - X^\mu Y^\nu \right)\tag{3}

よって，両辺は一致しました．これで式 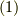(1) が示せました． 今日はここまで，お疲れさまでした．