この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
エルミート行列とユニタリー行列の関係

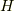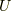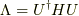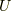量子力学でもお馴染みの話です． エルミート行列 H ならば，ユニタリー行列 U で挟むことによって対角化し，対角行列 \Lambda = U^\dagger H U とできます． では，逆にユニタリー行列 U で対角化できる行列 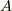A は，エルミート行列しかないの？ という疑問に答えるのがこの記事です．簡単の為，３次行列で話を進めます．

条件を整理する

列ベクトル 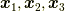\bm{x}_1,\bm{x}_2,\bm{x}_3 をユニタリー行列の成分とします． つまり，

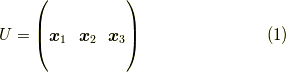
U = \begin{pmatrix} & & \\\bm{x}_1 & \bm{x}_2 & \bm{x}_3 \\ & & \end{pmatrix} \tag{1}

です．すると，その逆行列は，エルミート共役(共役転置)をダガー 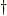\dagger で表すと，

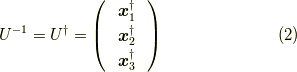
U^{-1}=U^\dagger = \begin{pmatrix} & \bm{x}_1^\dagger & \\ & \bm{x}_2^\dagger & \\ & \bm{x}_3^\dagger & \end{pmatrix} \tag{2}

となります．対角化された行列を次のように 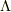\Lambda とします．

\Lambda = \begin{pmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{pmatrix} \tag{3}

さあ，準備ができた

すると， 正方行列の三連続積の展開 でやったように， 行列を展開 [*] できます．

[*]どうやらこれを，スペクトル展開と呼ぶようです．
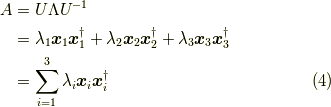
A &= U \Lambda U^{-1} \\&= \lambda_1 \bm{x}_1 \bm{x}_1^\dagger + \lambda_2 \bm{x}_2 \bm{x}_2^\dagger + \lambda_3 \bm{x}_3 \bm{x}_3^\dagger \\ &= \sum_{i=1}^3 \lambda_i \bm{x}_i \bm{x}_i^\dagger \tag{4}

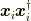この \bm{x}_i \bm{x}_i^\dagger はダイアド積と呼ばれる積です． 具体的に

\bm{x} = \begin{pmatrix}\alpha \\\beta \\\gamma \end{pmatrix} \tag{5}

と置くと， \ast を複素共役とするなら，

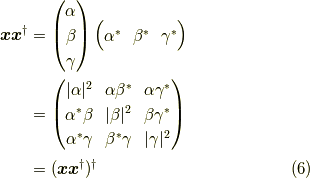
\bm{x}\bm{x}^\dagger &= \begin{pmatrix}\alpha \\\beta \\\gamma \end{pmatrix}\begin{pmatrix}\alpha^\ast & \beta^\ast & \gamma^\ast \end{pmatrix} \\&=\begin{pmatrix}|\alpha|^2 & \alpha \beta^\ast & \alpha \gamma^\ast \\\alpha^\ast \beta & |\beta|^2 & \beta \gamma^\ast \\\alpha^\ast \gamma & \beta^\ast \gamma & |\gamma|^2 \end{pmatrix} \\&= (\bm{x}\bm{x}^\dagger)^\dagger \tag{6}

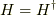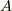となり，見事にこれは，エルミート行列の条件， H=H^\dagger を満たすことが分かります． その和である A も当然，エルミート行列です．

つまり，ユニタリー行列で対角化できるならば，その行列 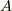A はエルミート行列であることが分かりました． [†]

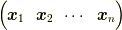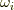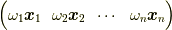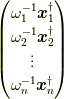[†]さらに強く言うなら，エルミート行列はユニタリー行列（別の言い方では，ユニタリー行列とは複素「正規」直交行列です．） \begin{pmatrix} \bm{x}_1 & \bm{x}_2 & \cdots & \bm{x}_n \end{pmatrix} ではなく，任意の複素数 \omega_i を各列に掛けた複素直交行列 \begin{pmatrix} \omega_1 \bm{x}_1 & \omega_2 \bm{x}_2 & \cdots & \omega_n \bm{x}_n \end{pmatrix} (ただし，その逆行列は \begin{pmatrix} \omega_1^{-1} \bm{x}_1^\dagger \\ \omega_2^{-1} \bm{x}_2^\dagger \\ \vdots \\ \omega_n^{-1} \bm{x}_n^\dagger \end{pmatrix} )でも，以上の議論は成立します．

今日はこの辺で，お疲れさまでした．