この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
続々々・ベクトルの回転
特定の向きを向いた剛体が,オイラー角と呼ばれる三つの回転を行った後の状態は, ある一つの軸まわりの回転で,同じ向きを向けることができます. その回転軸と回転の大きさを求めてみよう.というのが,今回の記事 です. ベクトルの回転 , 続ベクトルの回転 , 続々ベクトルの回転 の続編です.
オイラー角
オイラー角は,次の三つの行列の積で表されます.
この三回の回転で,どんな向きでも向くことができます.
詳しくは, 剛体のオイラー角でのハミルトニアン の慣性主軸の所をご覧ください.
また,式 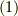 の二番目の等号が分からない方は 複雑な回転を基本的な回転で表す方法 も見ておくといいでしょう.
の二番目の等号が分からない方は 複雑な回転を基本的な回転で表す方法 も見ておくといいでしょう.
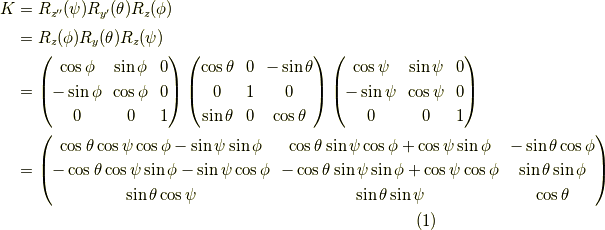
これと,今までこのシリーズで出てきた原点を通る軸周りの任意の大きさ 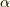 の回転行列,
の回転行列,
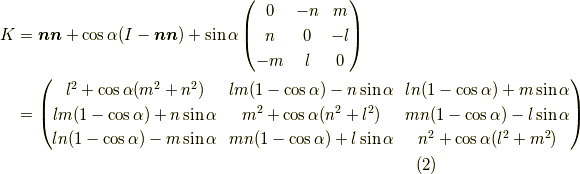
これらが等しいとするのです.
ここで,式(1),(2)のトレース(対角和)を取ります.  に注意すると,
に注意すると,
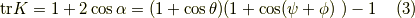
よって,
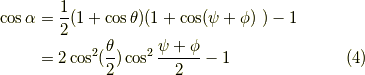
となります.ただし,恒等式 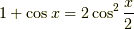 を
用いました.
を
用いました.  を求める為に対称成分の差を取ります.
を求める為に対称成分の差を取ります.
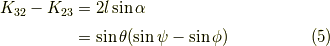
よって,
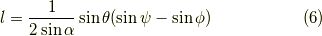
同様に,  についても,
についても,
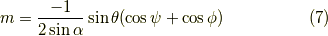
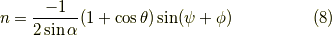
と求められます. 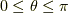 ,
, 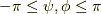 ですから,
ですから,
ここで, 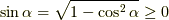 を用いて,
を用いて,
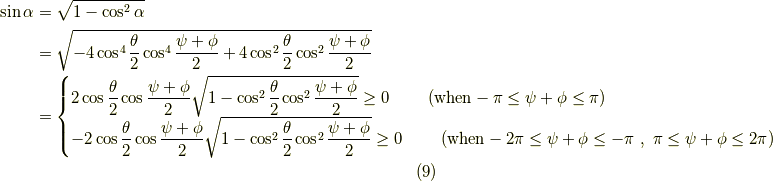
と,計算できます.そして,三角関数の和積の公式と半角の公式 [*] を用いてやると,
| [*] | 一応書いておきます. 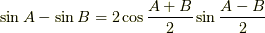 と
, と
, 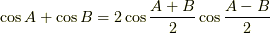 と
, と
, 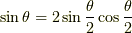 を用いました. を用いました. |
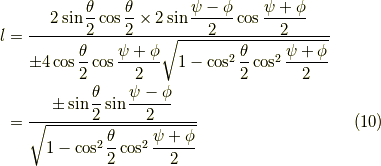
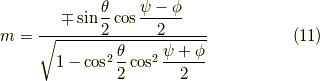
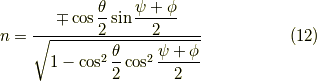
となり,(ただし,複号同順で,式(9)の符号と一致させます.)それなりにきれいな形になりました.
以上,回転の公式の対応の検証でした. 今日は,ここまで.