この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
速度場と輻射場
荷電粒子の運動による電磁場 では,荷電粒子が軌道 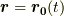 に沿って運動するときの点
に沿って運動するときの点  における電磁場を求めました.その結果は
における電磁場を求めました.その結果は
![\bm{E}(\bm{r}, t) = q \left[ \frac{(1-\beta^2)(\bm{n}-\bm{\beta})}{\kappa^3 R^2} \right]+ \frac{q}{c} \left[ \frac{\bm{n}}{\kappa^3 R} \times (\bm{n} - \bm{\beta}) \times \dot{\bm{\beta}} \right] \tag{1}](http://hooktail.maxwell.jp/kagi/e953811570a9d331ec4ff83bf8be4a04.png)
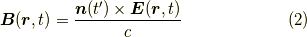
のようになるのでした.ここでは主に (1) について解説します.
二つの成分
![\bm{E}(\bm{r}, t) = q \left[ \frac{(1-\beta^2)(\bm{n}-\bm{\beta})}{\kappa^3 R^2} \right]+ \frac{q}{c} \left[ \frac{\bm{n}}{\kappa^3 R} \times (\bm{n} - \bm{\beta}) \times \dot{\bm{\beta}} \right] \tag{1}](http://hooktail.maxwell.jp/kagi/e953811570a9d331ec4ff83bf8be4a04.png)
式 (1) ですが,二つの項から成っています.
一つめの項は 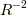 に比例する項です.
荷電粒子が等速度運動をしているときには,この項だけが電場に寄与します.
静電場でのクーロンの法則を一般化したような式ですね.
に比例する項です.
荷電粒子が等速度運動をしているときには,この項だけが電場に寄与します.
静電場でのクーロンの法則を一般化したような式ですね.
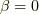 ならばクーロンの法則そのものになります.
この第一項は 速度場 (velocity field) と呼ばれます.
ならばクーロンの法則そのものになります.
この第一項は 速度場 (velocity field) と呼ばれます.
二つ目の項は 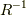 に比例する項です.
加速度を含んでいることに注意してください.
つまりこの項は荷電粒子が加速度をもって運動しているときにのみ値を持ちます.
第二項は 加速度場 (acceleration field) といいます.
に比例する項です.
加速度を含んでいることに注意してください.
つまりこの項は荷電粒子が加速度をもって運動しているときにのみ値を持ちます.
第二項は 加速度場 (acceleration field) といいます.
等速度運動しているときについて少し考えてみます.
荷電粒子が等速度 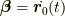 で運動しているとき,
時刻
で運動しているとき,
時刻 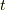 にある点
にある点  での電場は (1) から次のようになります.
での電場は (1) から次のようになります.
![\bm{E}(\bm{r}, t) = q \left[ \frac{(1-\beta^2)(\bm{n}-\bm{\beta})}{\kappa^3 R^2} \right]](http://hooktail.maxwell.jp/kagi/4e66de08286177acd19a4a497d5e396d.png)
このとき電場ベクトルは 現在の荷電粒子の位置 を向いています. 図を用いて考えて見ましょう.
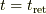 の荷電粒子の位置
の荷電粒子の位置 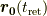 から観測点
から観測点  への変位
への変位 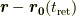 は
は
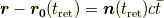
です.ただし 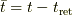 です.
です.
輻射場
電場の加速度場と,それに対応する磁場とをあわせて 輻射場 (radiation field)といいます.
![\bm{E}_{\rm rad}(\bm{r}, t) & = \frac{q}{c} \left[ \frac{\bm{n}}{\kappa^3 R} \times (\bm{n} - \bm{\beta}) \times \dot{\bm{\beta}} \right] \tag{3}\\\bm{B}_{\rm rad}(\bm{r}, t)& = \left[ \bm{n} \times \bm{E}_{\rm rad} \right] \tag{4}](http://hooktail.maxwell.jp/kagi/29011ebd1ed369ff230f6622d151d128.png)