この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
一般化されたエルミート多項式
この記事では,エルミート多項式を一般化します. 色々,遊んでいます.
準備
いきなりですが,次の演算子の変形ができます.
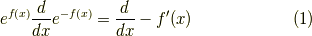
証明はフーリエ変換を使います.
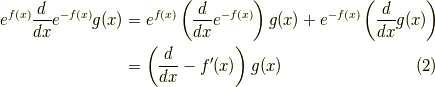
で,  は任意ですから,
は任意ですから,
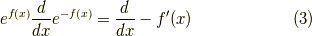
が言えました.さらには,
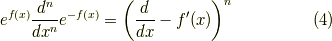
も自明です.
エルミート多項式
式 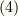 の演算子を
の演算子を 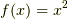 ,
, 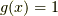 とし,調整の為
とし,調整の為 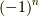 を掛けると,
を掛けると,
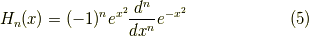
が得られ,また,
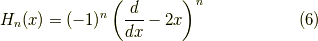
も出ます.式 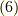 は変形して,漸化式,
は変形して,漸化式,
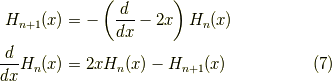
が得られます.
エルミート多項式の拡張
と言うことはです. 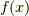 と
と 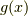 に好きな関数を入れてやれば,
エルミート多項式の拡張が容易に得られます.
に好きな関数を入れてやれば,
エルミート多項式の拡張が容易に得られます.
単純に 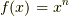 ,
, 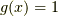 が直接的な拡張と言えるでしょう.
が直接的な拡張と言えるでしょう.
僕が気に入っているのは, 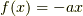 ,
, 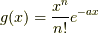 の時で,
これは
の時で,
これは 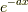 を無視して,
を無視して, 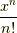 部分だけを微分する計算になります.
部分だけを微分する計算になります.
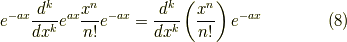
であり,
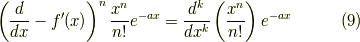
となります.
コメントをしておくと,僕は最初,線形代数のジョルダン標準形で出てくる,冪ゼロ因子の,
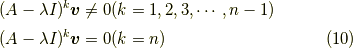
のアナロジー 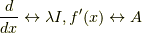 として,これを発見しました.
何か,面白い事が言えそうだと思っています.
として,これを発見しました.
何か,面白い事が言えそうだと思っています.
今日はここまで,お疲れさまでした!!