この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
フェルミオンの化学ポテンシャル
今回はフェルミオン(特に電子)の化学ポテンシャルがどんなものなのか, 統計力学的,物性論的に考えてみたいと思います. この話は土井正男『[物理の考え方2]統計力学』朝倉書店,2006年 を参考に書きました.
グランドカノニカル分布
グランドカノニカル分布とは,系を大きな環境(environment)と着目系(focused system)に分けて, エネルギーと粒子の交換を許す時の考え方です.
系の総粒子数を 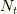 ,総エネルギーを
,総エネルギーを 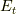 とし,
着目系には粒子数
とし,
着目系には粒子数 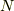 ,エネルギー
,エネルギー 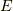 があるとします.
着目系の状態密度は
があるとします.
着目系の状態密度は 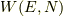 とし,
環境の状態密度は
とし,
環境の状態密度は 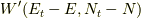 とします.
(なお,この本では状態数
とします.
(なお,この本では状態数 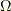 と状態密度
と状態密度 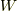 は,
共にエントロピーを表すのに,
は,
共にエントロピーを表すのに, 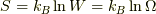 と
等式が成り立つことに言及しています. 下では
と
等式が成り立つことに言及しています. 下では 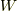 を用いて議論していますが,
を用いて議論していますが, 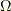 の方が適切かもしれません.
ただし,
の方が適切かもしれません.
ただし, 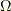 が
が 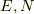 の非常に急激な増加関数なので,状態密度
の非常に急激な増加関数なので,状態密度 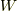 で議論しても成立はします.)
で議論しても成立はします.)
すると,着目系が 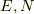 となる時の確率
となる時の確率 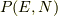 は,
は,
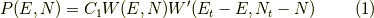
と表せます. ここと,以降でてくる 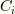 は規格化定数です.ここで,
は規格化定数です.ここで,
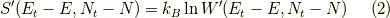
を使うと,式(1)は,
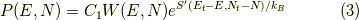
となります. 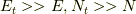 より,テイラー展開を使って,
より,テイラー展開を使って,
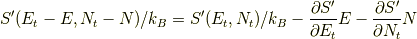
ここで,この話の要である次の公式を使います.環境系の温度を 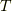 ,環境系の化学ポテンシャル
,環境系の化学ポテンシャル 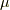 として,
として,

です.これは統計力学的には定義です.よって,
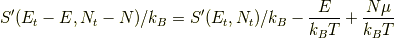
となります.
よって,逆温度 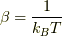 を用いて,式(1)は結局,
を用いて,式(1)は結局,
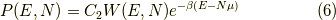
これがグランドカノニカル分布の考え方です.
つまり, 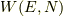 は着目系の
は着目系の 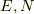 を持つ時の状態密度(状態数)ですから,
それ(
を持つ時の状態密度(状態数)ですから,
それ( 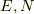 で指定される状態の集合)に含まれる一状態の実現確率が全て等しいとすると(等重率の原理),
一状態の実現確率
で指定される状態の集合)に含まれる一状態の実現確率が全て等しいとすると(等重率の原理),
一状態の実現確率 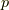 は,
は,
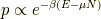
と言う,比例関係が成立します.
視点の転換
では,これが系の量子力学的一準位が着目系だったらどうでしょう?
その準位のエネルギーを  と考えます.
環境系はその系自身で,着目する準位と粒子とエネルギーの交換をするのです.
(この点に関しては,岩波基礎物理シリーズ7『統計力学』長岡洋介著のp.209を参考にしてください.)
と考えます.
環境系はその系自身で,着目する準位と粒子とエネルギーの交換をするのです.
(この点に関しては,岩波基礎物理シリーズ7『統計力学』長岡洋介著のp.209を参考にしてください.)
その規格化定数を 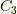 とすると,粒子が無い時,粒子がある時の
「確率」は,それぞれ
とすると,粒子が無い時,粒子がある時の
「確率」は,それぞれ
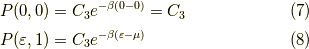
ですから,
着目準位に入る「粒子数の期待値」(確率ではない)は,
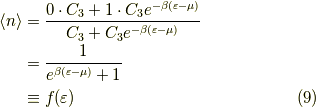
となります. 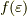 をフェルミ分布関数と言います.
そのエネルギーでの状態密度を量子統計力学らしく
をフェルミ分布関数と言います.
そのエネルギーでの状態密度を量子統計力学らしく 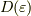 で表し,
またその系の最低準位を
で表し,
またその系の最低準位を 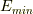 とすると,,
総粒子数
とすると,,
総粒子数 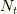 ,総エネルギー
,総エネルギー 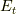 は,それぞれ,
は,それぞれ,
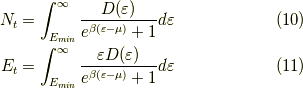
となります.
粒子数の保存
ここで,あるエネルギー  を基準にそれ以上にある粒子数
を基準にそれ以上にある粒子数 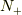 と,それ以下にあるホール数(空孔数)
と,それ以下にあるホール数(空孔数) 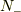 とすると,
とすると,
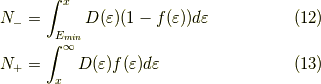
ここで, 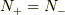 となる
となる  があります.よくよく考えるとそれはフェルミエネルギー
があります.よくよく考えるとそれはフェルミエネルギー 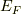 です.
つまり,全体の粒子数が変わらない限り,フェルミエネルギー以下の粒子が,下にホールを残し,上に励起されて存在する訳ですから,温度がどう変わっても,下のホール数と上の粒子数は同じです.
です.
つまり,全体の粒子数が変わらない限り,フェルミエネルギー以下の粒子が,下にホールを残し,上に励起されて存在する訳ですから,温度がどう変わっても,下のホール数と上の粒子数は同じです.
すると,
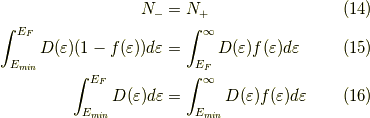
当然,これは総粒子数 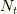 ですね.
ですね.
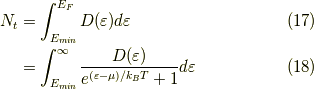
総エネルギー 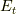 についても同様に,
についても同様に,
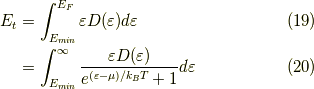
が成立します.変数は, 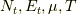 の四つであり,二式の条件があるので,
の四つであり,二式の条件があるので, 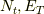 を指定すれば,
を指定すれば, 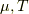 が決定されます.
が決定されます.
粒子数変化と化学ポテンシャル,温度の関係
定性的な考察をしておきましょう.
式(18)について,温度 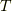 を一定にして粒子数
を一定にして粒子数 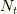 を増大させることは,ドーピングであり,フェルミエネルギー
を増大させることは,ドーピングであり,フェルミエネルギー 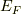 を増大させることになります.ここで,被積分関数で変わりうるのは,フェルミ分布関数
を増大させることになります.ここで,被積分関数で変わりうるのは,フェルミ分布関数
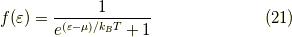
のみです.化学ポテンシャルの増大は全ての  で分布関数の大きさを増大させますから,結局,粒子数の増大は化学ポテンシャルの増大を引き起こします.一方,エネルギー準位を小さいところから大きい方へ見ていくと,その準位の粒子数は減っていきます.これは指数関数の肩の
で分布関数の大きさを増大させますから,結局,粒子数の増大は化学ポテンシャルの増大を引き起こします.一方,エネルギー準位を小さいところから大きい方へ見ていくと,その準位の粒子数は減っていきます.これは指数関数の肩の  と
と 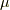 の符号の違いとなって表れています.
の符号の違いとなって表れています.
余談ですが,金属のフェルミ準位,言い換えて,フェルミ温度 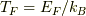 は数万ケルビンに相当するそうです.
そこから言える事は,まずフェルミ温度以上の温度とは,フェルミ統計でなくボルツマン統計で有効となる(上手く記述できる)温度です.また,常温程度では金属はフェルミ縮退を起こしている事が分かり,つまり,温度上昇と共に電子比熱が上昇していく(電子の励起先準位が空になり電子を受け入れ可能になっていく)ことが分かります.また,純粋な化学ポテンシャルの変化は,フェルミ分布関数の
は数万ケルビンに相当するそうです.
そこから言える事は,まずフェルミ温度以上の温度とは,フェルミ統計でなくボルツマン統計で有効となる(上手く記述できる)温度です.また,常温程度では金属はフェルミ縮退を起こしている事が分かり,つまり,温度上昇と共に電子比熱が上昇していく(電子の励起先準位が空になり電子を受け入れ可能になっていく)ことが分かります.また,純粋な化学ポテンシャルの変化は,フェルミ分布関数の  方向の平行移動となり,純粋な温度下降はフェルミ分布関数の
方向の平行移動となり,純粋な温度下降はフェルミ分布関数の 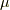 付近における急激な減少をメインに起こします.またこの時,状態密度の様子によって,温度が変化すると化学ポテンシャルは変化するという副作用もあります.絶対零度における化学ポテンシャルの事をフェルミエネルギーと言います.
付近における急激な減少をメインに起こします.またこの時,状態密度の様子によって,温度が変化すると化学ポテンシャルは変化するという副作用もあります.絶対零度における化学ポテンシャルの事をフェルミエネルギーと言います.

という化学ポテンシャルの関係式より,粒子の追加で,粒子数 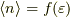 が最も
増大するのは
が最も
増大するのは 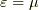 付近なので,化学ポテンシャルは「一粒子を追加するのに必要なエネルギー」だと言う事が出来ます.特に絶対零度では化学ポテンシャルはフェルミエネルギーと言われますが,一粒子追加のエネルギーの増大がフェルミエネルギーに等しいとはっきり分かります.逆に温度が高いと,一粒子追加のエネルギーと化学ポテンシャルの対応ははっきりしなくなってくるのではないでしょうか.
付近なので,化学ポテンシャルは「一粒子を追加するのに必要なエネルギー」だと言う事が出来ます.特に絶対零度では化学ポテンシャルはフェルミエネルギーと言われますが,一粒子追加のエネルギーの増大がフェルミエネルギーに等しいとはっきり分かります.逆に温度が高いと,一粒子追加のエネルギーと化学ポテンシャルの対応ははっきりしなくなってくるのではないでしょうか.
筆者の勘違い
僕はいつの間にか勘違いをして,

という関数がなんらか意味を持つと思っていましたが,
よくよく考えると全くの勘違いの様です.
こんな関数は意味を持ちません.むしろ 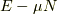 が意味を持つのは,
次の意味です.
が意味を持つのは,
次の意味です.
熱・粒子浴内にある開放系を考えます.ここで着目系を一準位の集合とします.
熱浴に対しては小さいが,一粒子に比べたらマクロと見なせる複数の一準位の集合を部分系として 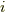 でラベルします.その実現確率
でラベルします.その実現確率 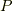 は,部分系
は,部分系 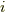 がエネルギー
がエネルギー 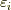 ,粒子数
,粒子数 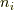 を持つとして,粒子の区別がつけず,独立事象として扱えば,(つまり,量子論的に扱って)
を持つとして,粒子の区別がつけず,独立事象として扱えば,(つまり,量子論的に扱って)
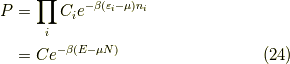
と言う「確率」として出てきます. 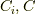 は
は 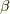 や
や 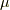 に依らない規格化定数で,
に依らない規格化定数で,
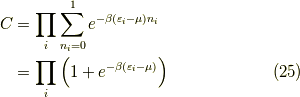
です.洒落た本だと,トレースを使って
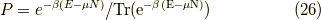
として出てくることがあります.気持ちとしては,
(逆)温度 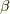 ,化学ポテンシャル
,化学ポテンシャル 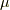 の環境に置かれた状態が
エネルギー
の環境に置かれた状態が
エネルギー 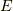 ,粒子数
,粒子数 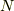 を持つ時の実現「確率」(粒子数期待値ではない)と言う事です.
を持つ時の実現「確率」(粒子数期待値ではない)と言う事です.
その他の注意
自由電子ガスの化学ポテンシャルのゾンマーフェルト展開では"温度上昇"が,化学ポテンシャルの減少を引き起こします.勘違いしやすいところだと思うのですが,一方,"粒子密度上昇"によっては,化学ポテンシャルは増加するのみです.
それでは,今日はこの辺で.お疲れ様でした.