この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ビオ・サバールの法則とその応用
円電流の作る磁場をビオ・サバールの法則を用いて直接積分して求めます.
導入
電流は流れるとき,必ず磁場を伴って流れています. それを表す法則は,ふたつありまして, 一方は「アンペールの法則」,もう一方は,「ビオ・サバールの法則」と呼ばれています. ここでは,ビオ・サバールの法則を使って,簡単な例に適用してみます.
ビオ・サバールの法則
原点に微小な電流要素 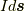 を考えます.ただし
を考えます.ただし 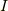 は電流の大きさで,微小方向ベクトルは電流の向きを表す方向
ベクトル
は電流の大きさで,微小方向ベクトルは電流の向きを表す方向
ベクトル 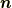 を用いて,
を用いて, 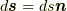 と表される.この微小電流要素が,位置
と表される.この微小電流要素が,位置  に作る磁場
に作る磁場 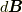 は,
は,

となります.ただし 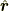 は位置ベクトル方向を向いた単位ベクトルとしました.
は位置ベクトル方向を向いた単位ベクトルとしました.
円電流が作る磁場
いまxy平面内に半径  の円電流を考えます.この円電流が作る磁場をビオ・サバールの法則で計算してみます.
の円電流を考えます.この円電流が作る磁場をビオ・サバールの法則で計算してみます.
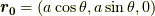 にある微小電流が (この時,微小接線ベクトル
にある微小電流が (この時,微小接線ベクトル 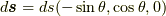 です)
です) 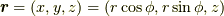 の位置
に(最後は円筒座標を使いました)作る磁場は,式 (1) より,
の位置
に(最後は円筒座標を使いました)作る磁場は,式 (1) より,
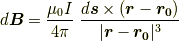
今,
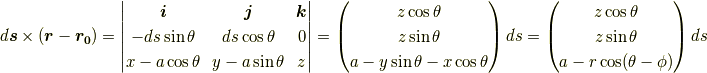
で,
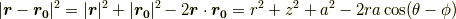
です.これを用いて,まずz方向の磁場 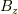 を求めます.微小距離
を求めます.微小距離 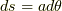 と置けるのでθの積分にすることができて,
と置けるのでθの積分にすることができて,
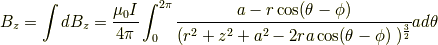
同様にx方向,y方向も書くと,
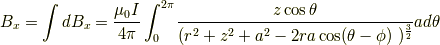
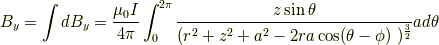
です.おそらくこの積分は解けません.
円電流が作る磁場(原点では)
解けないとは言いましたが,二つの特別な場合を計算してみます.
まず  の時は簡単です.まずz方向について見てみます.
の時は簡単です.まずz方向について見てみます.
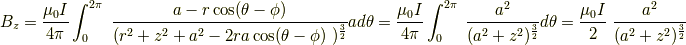
となり,またx方向,y方向は対称性から0になります.
さらに特別な場合,コイルの円の中心 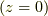 では
では 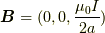 となります.
となります.
円電流が作る磁場(十分に遠方では)
十分に遠方 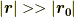 では,分母を近似することができます.
では,分母を近似することができます.
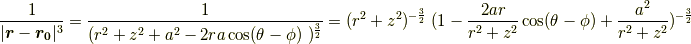
ここで 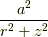 は二次の微小量なので無視し,テイラー展開
は二次の微小量なので無視し,テイラー展開 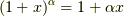 を用いると,
を用いると,
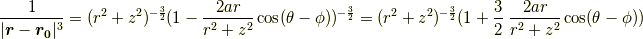
となります.これを用いてz方向成分を求めると,
![B_z &= \frac{\mu_0I}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 (a-r \cos (\theta -\phi))(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi))a d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 r(- \cos (\theta -\phi)+\frac{a}{r})(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi)) d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 r(-1+\frac{3a^2}{r^2+z^2})\cos (\theta -\phi) +a -\frac{3ar^2}{r^2+z^2}\cos^2 (\theta -\phi) d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} [ ar(\frac{1}{r} -\frac{3r}{2(r^2+z^2)}) (\theta-\phi) ]^{2\pi}_0 \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \{ 2\pi ar (\frac{r^2+z^2}{r(r^2+z^2)}-\frac{\frac{3}{2}r^2}{r(r^2+z^2)})\} \\&= \frac{\mu_0Ia}{2(r^2+z^2)^{\frac{3}{2}}} ( ar \frac{z^2-\frac{1}{2}r^2}{r(r^2+z^2)}) \\&= \frac{\mu_0Ia^2}{2(r^2+z^2)^{\frac{5}{2}}} (z^2-\frac{1}{2}r^2)](http://hooktail.maxwell.jp/kagi/af4a9c80fbf80ee52b9675259ce80111.png)
ふう疲れた,とにかくこうなるわけですよ.
まだ,x方向とy方向が残っています.でも安心してください.x方向は  を
を  で置き換えるだけです.
で置き換えるだけです.
![B_x &= \frac{\mu_0I}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi))a d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3a}{r^2+z^2} r\cos (\theta - \phi)) d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3a}{r^2+z^2} (x \cos \theta + y \sin \theta) d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z (\cos \theta +\frac{3ax}{r^2+z^2} \cos^2 \theta + \frac{3ax}{r^2+z^2} \sin \theta \cos \theta) d \theta \\&= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} [ z \frac{3ax}{2(r^2+z^2)} \theta ]^{2\pi}_0 \\&= \frac{3\mu_0Ia^2xz}{4 (r^2+z^2)^{\frac{5}{2}}}](http://hooktail.maxwell.jp/kagi/bd343b76662250a5059915f19ebba097.png)
y方向についてはこれのxをyで,yはxで 置き換えればいいので,
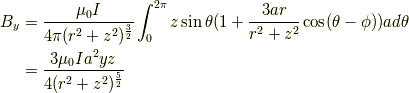
まとめると,
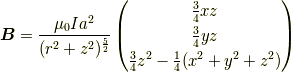
であり,成分としてまとめると,
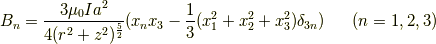
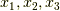 は,それぞれ
は,それぞれ  をあらわし,
をあらわし, 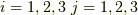 にたいし
にたいし
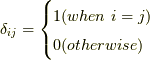 となり,これはクロネッカーのデルタという名前です.
となり,これはクロネッカーのデルタという名前です.