この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
行列の指数関数のラプラス変換
指数関数 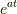 のラプラス変換は
のラプラス変換は 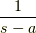 であり,有名です.では,任意の正方行列
であり,有名です.では,任意の正方行列 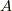 に対する行列の指数関数
に対する行列の指数関数 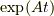 をラプラス変換するとどうなるか?と言うのが今回の話です.
をラプラス変換するとどうなるか?と言うのが今回の話です.
結果
まずは結果から言ってしまいましょう.
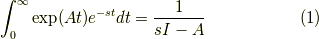
が成立します.ここで左辺は行列 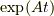 のそれぞれのラプラス変換を取るものとします.右辺は逆数ではなく逆行列
のそれぞれのラプラス変換を取るものとします.右辺は逆数ではなく逆行列 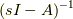 のことです.そうは言われてもどう考えていいか分からないでしょう.
のことです.そうは言われてもどう考えていいか分からないでしょう.
そこで証明します.それには,これよりも弱い主張である,正方行列 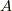 を対角化したもの,もしくは,ジョルダン細胞
を対角化したもの,もしくは,ジョルダン細胞 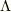 に変えて考えます.
に変えて考えます.
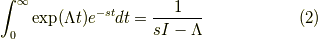
ちなみに任意の複素正方行列はジョルダン標準形,つまり対角化,もしくはジョルダン細胞をブロック対角成分に並べた形に変形できます.
(i)Λが対角化される場合
まず,定数  を定数として
を定数として  次複素正方行列
次複素正方行列 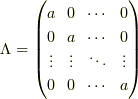 の時を考えます.
の時を考えます.
この時,
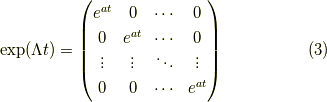
となります.このラプラス変換なのですが,式(2)の左辺が
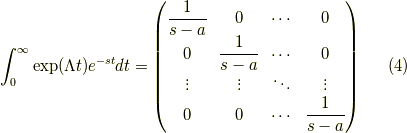
であり,右辺は 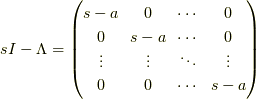 の逆行列ですから,
の逆行列ですから,
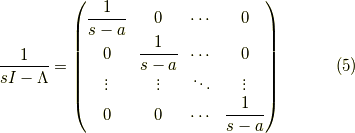
となり一致し,式(2)が示されました.
(ii)Λがジョルダン細胞になる場合
- この場合,ちょっと大変です.
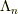 が
が  次のジョルダン細胞
次のジョルダン細胞 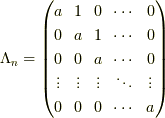 に対して,拙記事 ジョルダン細胞のn乗 で示したように
に対して,拙記事 ジョルダン細胞のn乗 で示したように
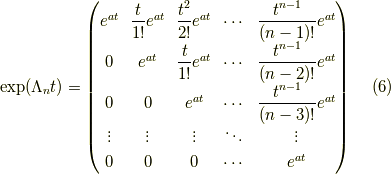
これをラプラス変換すると
![\mathcal{L}[t^n e^{at}] &= \left( -\dfrac{d}{ds} \right)^n \mathcal{L}[e^{at}] \\&= \dfrac{(n!)}{(s-a)^{n+1}}\tag{7}](http://hooktail.maxwell.jp/kagi/87cb2fd13ad943ae16b753744867e4d3.png)
ですから,
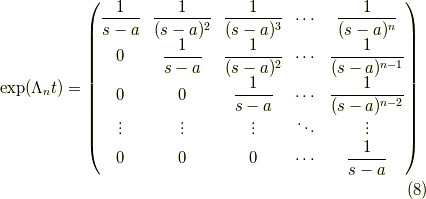
となります.
結構大変な逆行列の計算
一方,右辺について
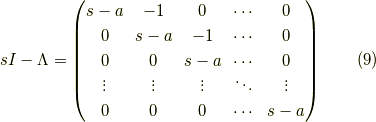
です.その逆行列は

となります.これを示します.証明には数学的帰納法を用います.
まずは  次のジョルダン細胞に似た次の式
次のジョルダン細胞に似た次の式 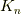 について列基本変形を考えます.
について列基本変形を考えます.
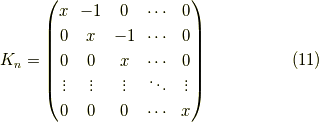
とすると,
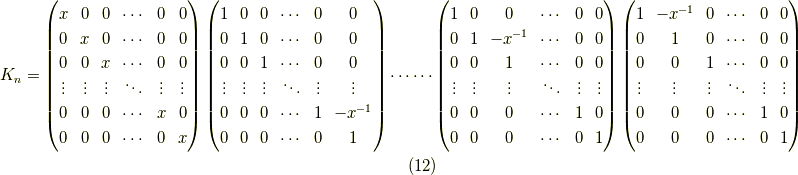
と分解できます.よって,  の逆行列は
の逆行列は

となります.ここで,  次正方行列
次正方行列 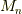 を次のように定義します.
を次のように定義します.
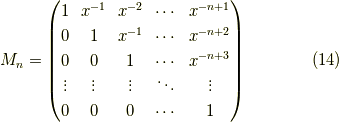
この時,全ての自然数  に対して,
に対して,

が成立する事を示します.
(ア) 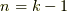 の時,
の時, 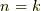 でも成立する事を示す.
でも成立する事を示す.

が成立するとします.この時, 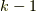 次列ベクトル
次列ベクトル 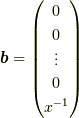 を用いて,
を用いて,
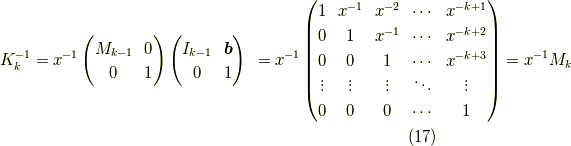
となります.
(イ) 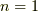 の時
の時

これは成立する.つまり,(ア)と(イ)から全ての自然数  に対して式(15)が成立する事が示せました.この式(15)で
に対して式(15)が成立する事が示せました.この式(15)で 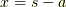 を代入すると,式(11)と式(15)がそれぞれ式(9)と式(10)になります.よって,式(8)と式(10)は等号で結ばれ,無事式(2)が示せました.
を代入すると,式(11)と式(15)がそれぞれ式(9)と式(10)になります.よって,式(8)と式(10)は等号で結ばれ,無事式(2)が示せました.
最後の仕上げ
ここまで示せれば,あとはもう少しです.正方行列 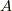 をジョルダン標準形
をジョルダン標準形 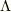 に変形する正則行列
に変形する正則行列 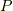 とすると,
とすると,

ですから,
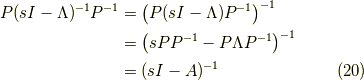
と言う式と,ラプラス変換の線形性から,式(2)の左から 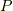 を,右から
を,右から 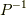 を掛ければ,式(1)が導けます.
を掛ければ,式(1)が導けます.
今日はこの辺で,お疲れ様でした!!