この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
リー環の随伴表現とは
リー環とは
リー環,もしくは,同じものですがリー代数 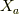 において,交換子から定まる構造定数
において,交換子から定まる構造定数 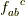 を
次の様に定めます.
を
次の様に定めます.
![[X_a,X_b] = i f_{ab}^{ \ \ c} X_c \tag{1}](http://hooktail.maxwell.jp/kagi/b84c356feabe12ef0ad20f9c81e04419.png)
ここで, 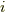 は虚数単位で,交換子は
は虚数単位で,交換子は ![[X_a,X_b] = X_a X_b - X_b X_a](http://hooktail.maxwell.jp/kagi/52bc2bff4451b2300547f6f96482c017.png) を表します.
また,アインシュタインの縮約規則を用いて,
を表します.
また,アインシュタインの縮約規則を用いて,  は全ての元にわたる和です.
は全ての元にわたる和です.
リー環というと,特定の代数演算の関係が決められた抽象的な
代数ですが,それと同じ関係を満たす行列で具体的に表すことができます.
その代数の行列化をリー環の「表現」と言います.
表現にはいろいろな種類がありますが,その中で今回は随伴表現 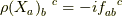 というものを紹介します.
ここで,
というものを紹介します.
ここで, 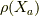 は表現(行列)で
は表現(行列)で 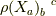 は行列の成分で
は行列の成分で  は行列の行,
は行列の行,  は行列の列を指定します.
不思議な事にこれは元のリー環の一つの表現になっているのです.
は行列の列を指定します.
不思議な事にこれは元のリー環の一つの表現になっているのです.
ヤコビ積
リー環には,交換子からなるヤコビ恒等式があります. それは,
![Z = [X_a,[X_b,X_c]] + [X_a,[X_b,X_c]] + [X_a,[X_b,X_c]] = 0 \tag{2}](http://hooktail.maxwell.jp/kagi/c43c45f4bf11e37b765f3bd7691c8f8f.png)
という任意のリー環に対して恒等的に成り立つ関係式です.
ただし,右辺の 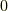 はリー環のゼロ元です.
この関係は,実際に行列を持ち出すことなく,
代数的に展開してやれば,確認できます.
はリー環のゼロ元です.
この関係は,実際に行列を持ち出すことなく,
代数的に展開してやれば,確認できます.
さて,式 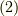 を式
を式 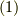 の関係を用いて,
変形していきましょう.
の関係を用いて,
変形していきましょう.
![[X_a,[X_b,X_c]] &= [X_a,i f_{bc}^{ \ \ d} X_d] \\&= i f_{bc}^{ \ \ d} [X_a,X_d] \\&= i^2 f_{bc}^{ \ \ d} f_{ad}^{ \ \ e} X_e \\&= - f_{bc}^{ \ \ d} f_{ad}^{ \ \ e} X_e\tag{3}](http://hooktail.maxwell.jp/kagi/3259ddc28a80a5da4a7eddc5356c0a39.png)
の様に計算していくと,ヤコビ恒等式は,
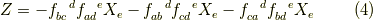
ここで,任意の  に対して,上式は成立するので,
に対して,上式は成立するので, 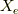 を除いて,
を除いて,
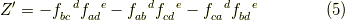
随伴表現
さて,随伴表現との対応を見てみましょう.

の様に決めると,式 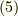 は,
は,
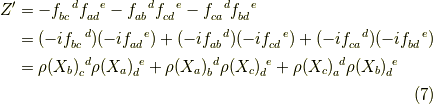
ここで全体の符号を反転させて, 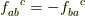 の関係を使うと(これは構造定数が交換子から作られていて,
の関係を使うと(これは構造定数が交換子から作られていて, ![[X_a,X_b] = - [X_b,X_a]](http://hooktail.maxwell.jp/kagi/d50f50e63f66c944d602fe95530a3781.png) であることから出ます.),
であることから出ます.), 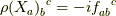 より
より 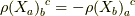 が言えるので,
が言えるので,
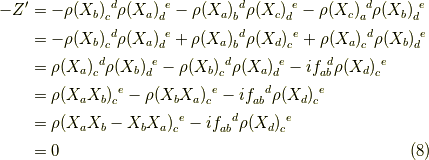
となり,よって,
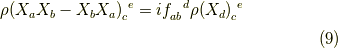
ですから,これは,リー環が満たす代数関係
![[X_a,X_b] = X_a X_b - X_b X_a = i f_{ab}^{ \ \ d} X_d\tag{10}](http://hooktail.maxwell.jp/kagi/af25761d4a7daa82357da9af1ee9a3a4.png)
に対応しています.(単連結な)リー代数の構造は構造定数によって,
完全に決定されます.よって, 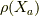 はリー環の表現だと分かります.
はリー環の表現だと分かります.
具体例(su(2)とso(3))
最後に具体例として,同じ構造定数を持つ 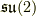 と
と 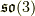 の随伴表現を
見て終わりにします.その構造定数は例えば,パウリ行列
の随伴表現を
見て終わりにします.その構造定数は例えば,パウリ行列 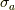 が
が
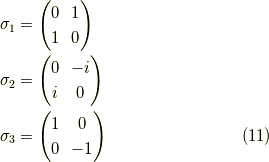
で,

とすれば,
![[X_1,X_2] &= i X_3 \\[X_2,X_3] &= i X_1 \\[X_3,X_1] &= i X_2 \tag{13}](http://hooktail.maxwell.jp/kagi/fd6eef56f018282a2a2ea3c5ff708d64.png)
より,ゼロにならないのは,
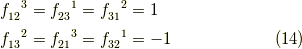
と分かるので,随伴表現の行列 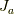 は,
は,
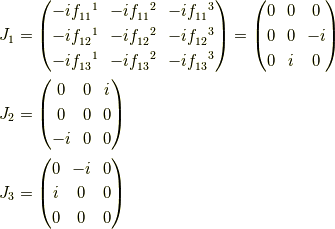
より,随伴表現が表現として成立しているか確かめると, 確かに例えば,
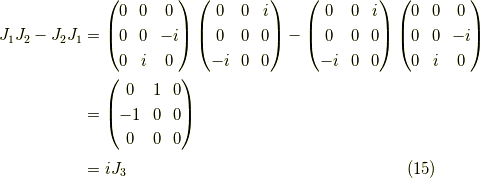
となり,確かに元のリー代数と同じ構造定数を持つ表現になっていることが分かります.