この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ルジャンドル変換で結ばれた四つのエネルギー関数
この記事ではラグランジアン  とハミルトニアン
とハミルトニアン 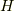 のルジャンドル変換を
のルジャンドル変換を
応用して, 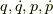 の間の変換行列を求めます.
の間の変換行列を求めます.
復習
まず,微分形がはっきりしている,ハミルトニアン 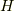 の微分を求めます.
の微分を求めます.
ハミルトニアンは
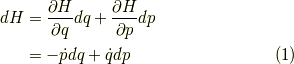
ハミルトニアンの自然な変数は 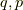 です.(
です.( 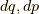 の式だからです.)
の式だからです.)

が言えます.次にラグランジアンを調べます.
すると,  ですから,
ですから,
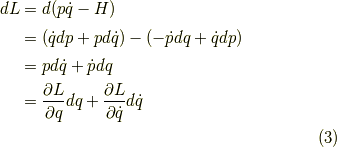
となり,ラグランジアンの自然な変数は 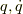 です.
です.

この形から 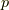 を消去すると,オイラーラグランジュ方程式が得られます.
を消去すると,オイラーラグランジュ方程式が得られます.
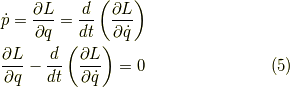
運動に関する情報は全て  に入っています.ルジャンドル変換は情報を落とさないので,
に入っています.ルジャンドル変換は情報を落とさないので,
他のエネルギー関数についても同様です.
新しいエネルギー関数
ラグランジアンからハミルトニアンを求めるとき, 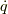 を消去して
を消去して 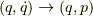 の変数変換を行いました.
の変数変換を行いました.
それならば,次の様にしては如何でしょう?
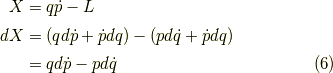
こうすると, 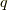 を消去して
を消去して 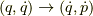 の変数変換を行ったことになります.
式
の変数変換を行ったことになります.
式 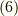 からは,
からは,

この関数 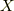 は今回はあまり重要ではありません.
欲しいのは
は今回はあまり重要ではありません.
欲しいのは 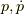 を変数に持つ関数です.
それを
を変数に持つ関数です.
それを 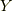 とすると,
とすると,
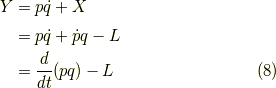
すると,その微分は
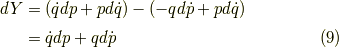
となり,

となります.
オイラーラグランジュ方程式をこれに対しても作ることが出来て,

となります.
変換行列
本来  で書かれる
で書かれる 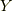 を
を 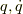 で書けると便利です.
その変換行列はヤコビ行列,
で書けると便利です.
その変換行列はヤコビ行列,
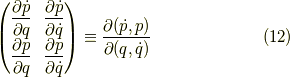
で書けます.これとその逆行列を求めるのがこの記事の主内容です.
訳あって行ベクトルで書きますが, これが出来ると,
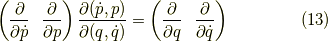
より,
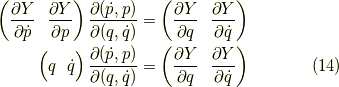
などと出来ます.
ここで  の微分をリストにしておきます.
の微分をリストにしておきます.

です.式  は次のように書けます.
は次のように書けます.

一価関数の偏微分は交換できることを使いました. この逆行列はどうなるでしょう?
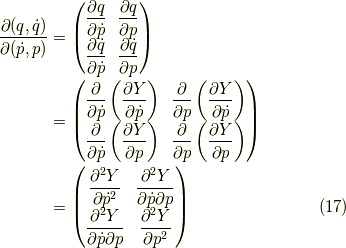
よって,
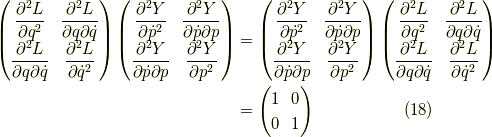
が成立します.
後は,他にも  など欲しいかもしれません.
など欲しいかもしれません.
ここで,何が独立変数で何が従属変数なのか,整理して
おきましょう.  は,
は,  の関数で,
の関数で,
分子は引数を明示すると 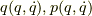 の引数を取る関数です.
の引数を取る関数です.
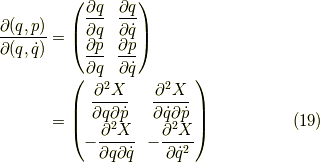
逆行列は,
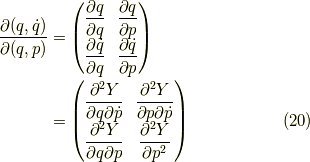
となります.注意として,偏微分をする際の固定方向が異なる為に, 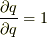 等は言えないようです
等は言えないようです
これらの行列は,偏微分演算子の行ベクトルに対してだけでなく,
例えば,式 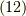 だと微分の列ベクトルに対しても,
だと微分の列ベクトルに対しても,

等と言う使い方もできます.
今まで,これらの変換は,専ら 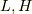 の偏微分だけで考えていましたが,
の偏微分だけで考えていましたが,
この記事によれば, 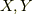 も用いることでより便利に扱えます.
も用いることでより便利に扱えます.
具体例(調和振動子)
具体的な例で結果を確認しておきましょう. 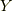 は,
は,  で表すべき関数で,
で表すべき関数で,

とすると,

より,

だから,これを解くと,
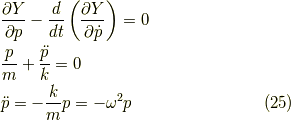
となり,確かに,
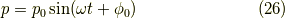
と振動解が得られます.
今日はこの辺で,お疲れさまでした.