この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
慣性モーメント
剛体の回転シーリズ第5弾です.前の記事は 全角運動量 です. 次の記事は 加速度座標系と慣性力 です.
球体の回転
前々回の記事では,xy平面内の回転しか扱いませんでした.
今回は,xy平面内以外の運動を考えてみます.
原点に角速度ベクトル 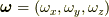 の回転をする
質量密度
の回転をする
質量密度 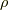 で一様な,半径
で一様な,半径 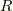 の球体を考えます.
の球体を考えます.
ここで,位置 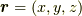 にある微小要素
にある微小要素 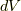 (質量
(質量 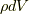 )を考えます.
角速度ベクトルは
)を考えます.
角速度ベクトルは 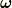 ですから,その速度は
ですから,その速度は 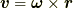 です.
角運動量 [*] は,
です.
角運動量 [*] は,
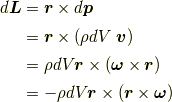
です.この形の式は 続ベクトルの回転 を参考にすると この式を扱うのに役に立つのではないでしょうか. 行列を用いると,この形を扱うのが容易になるということが書いてあります.
| [*] | この角運動量は,連続体の場合を考えています.質点からなる物体の角運動量は,  となります. となります. |
慣性テンソル
そこで,行列(テンソル)を用いて 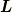 の成分を
の成分を 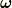 の成分の関数として
式を表してみます.
すると,
の成分の関数として
式を表してみます.
すると,
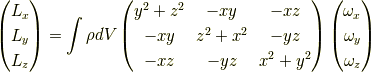
これを

と書きます.
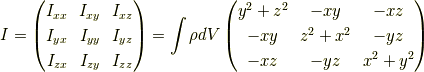
を慣性テンソルといいます.厳密に言うと行列と(二階の)テンソルは別の概念です.
詳しくは ベクトル解析 のテンソル代数をご覧ください.テンソルを行列の形を借りて
書き下したのが上の式です.ここで,対角項 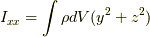 などを
慣性モーメントと呼び,非対角項
などを
慣性モーメントと呼び,非対角項 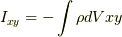 等を慣性乗積といいます.
これは,微小質量
等を慣性乗積といいます.
これは,微小質量 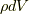 の時だけでなく,この
の時だけでなく,この 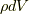 を有限質量
を有限質量  で置
き換えた時も同じ呼び方をします.慣性モーメントは一乗か二乗かの違いこそあれ,
ある物理量(質量)と,ある点からの距離の二乗の積になっていて,
どの点の周りを考えるかによって異なる量なので,確かにモーメントの一種ですね.
で置
き換えた時も同じ呼び方をします.慣性モーメントは一乗か二乗かの違いこそあれ,
ある物理量(質量)と,ある点からの距離の二乗の積になっていて,
どの点の周りを考えるかによって異なる量なので,確かにモーメントの一種ですね.
そして,慣性テンソルをテンソルとして書き下すなら,
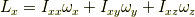
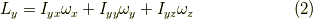
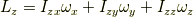
と書くのが一般的かと思います.
式をちょっとみてみればわかりますが,一般に 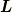 と
と 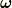 は違う方向
を向いています.
は違う方向
を向いています. 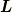 と
と 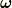 が
違う方向を向いている時には外力を加えて,回転を維持しなければなりません.
が
違う方向を向いている時には外力を加えて,回転を維持しなければなりません.
簡単なイメージを書いておくと,慣性モーメントは物体の回りにくさを,もしくは,
同じ回転にたいするその物体が持つエネルギーの大きさを表す量であり,
慣性乗積は,どれだけ 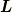 と
と 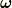 の向きがずれてくるかを表していると言えるでしょう.
の向きがずれてくるかを表していると言えるでしょう.
慣性テンソルに関する定理1
ここで慣性テンソル 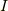 は対称行列ですから,
ある直交行列
は対称行列ですから,
ある直交行列 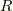 で対角化できます.
つまり,うまく直交座標系を選べば,慣性乗積はすべて0になります.
そのとき出てくる対角化された慣性テンソル
で対角化できます.
つまり,うまく直交座標系を選べば,慣性乗積はすべて0になります.
そのとき出てくる対角化された慣性テンソル 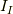 は,次のような成分
を持ちます.
は,次のような成分
を持ちます.
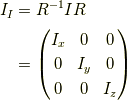
出てきた対角成分 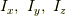 を主慣性モーメントと呼びます.
それが成り立つ座標系を慣性主軸といいます.
を主慣性モーメントと呼びます.
それが成り立つ座標系を慣性主軸といいます.
再び球体の回転
今考えていたのは,微小要素 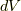 の作る角運動量でした.
角運動量はベクトルですから足し合わせることができます.
ここで,密度
の作る角運動量でした.
角運動量はベクトルですから足し合わせることができます.
ここで,密度 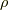 が一様で回転する球体を考えます.
全体の作る角運動量を求めるには半径
が一様で回転する球体を考えます.
全体の作る角運動量を求めるには半径 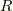 の球形領域で積分すれば求められます.
の球形領域で積分すれば求められます.
極座標を用いて式 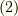 を積分します.
まず
を積分します.
まず 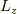 を積分します.
を積分します.
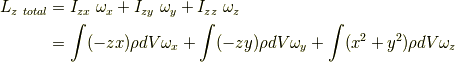
この計算には  や
や 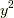 ,
, 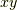 の球形領域での積分が必要です.
の球形領域での積分が必要です.
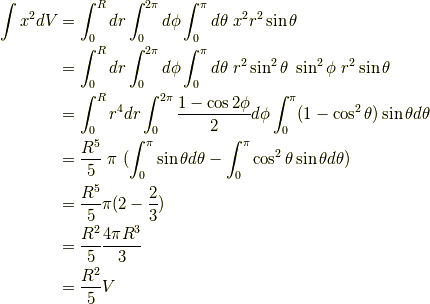
 は球の体積です.
は球の体積です.
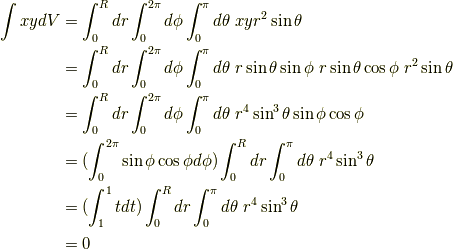
対称性から
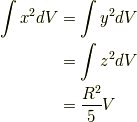
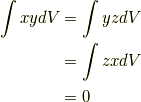
よって,

 に注意してください.
に注意してください.  は球体の質量です.
こうして結果が出たのですが,回転する球体は球の対称性により
は球体の質量です.
こうして結果が出たのですが,回転する球体は球の対称性により 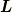 と
と 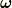 の
方向が一致することがわかりました.
の
方向が一致することがわかりました.
球の位置が原点にない時
ここから先はおまけのようなものです.すこし一般化してみます.
回転する球が,原点になく( 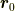 にあり)しかも重心が速度
にあり)しかも重心が速度 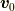 をもって
移動している時はどんな角運動量をもつのでしょうか?
をもって
移動している時はどんな角運動量をもつのでしょうか?
やはり微小体積 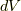 の持つ角運動量を積分します.
こんどは位置が
の持つ角運動量を積分します.
こんどは位置が  から
から 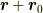 に替わり,
速度は
に替わり,
速度は 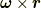 から
から  に替わります.
よって,
に替わります.
よって,
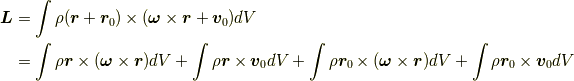
最後の変形のうち,第一項は最初に考えた例と同じ値を持ちます. これは原点に対する角運動量の内,球の位置を変えても一定の値を持つ部分です. 次に第二項は定ベクトルと球内の位置ベクトルの積の積分なので一次の項になります から,ゼロになります. そして第三項は第二項と同様の理由でゼロになります. 最後に第四項は回転しない粒子が原点に対してもつ角運動量と同じ値をもちます. これは粒子の位置,速度によります.
第一項の回転する粒子が持つ角運動量は, 一つ前の記事で扱った回転しあう二粒子の角運動量同様に 位置を変えても一定の値を持つという特別な性質を持ちます. 複数の角運動量はベクトルなので足し合わせられるというのも重要な性質です. 粒子が自転しながら軌道上を動くときには,その全体としての角運動量は, 軌道による角運動量と自転による角運動量の和になります.
この応用として角運動量は,量子力学で原子の軌道角運動量や電子のスピン角運動量 としてでてきます.角運動量の合成を学ぶ時にはこの記事のことを思い出していただけたら 嬉しいです.
続きは こちら
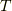 を計算しておきます.
を計算しておきます.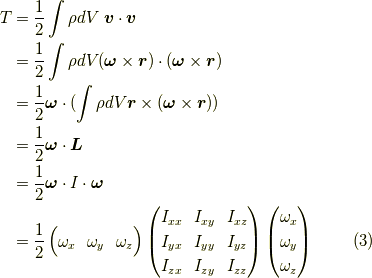
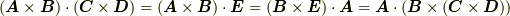 という公式を用いました.
という公式を用いました.