この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
スピンの回転の数理
この記事は,スピノールの回転がなぜ
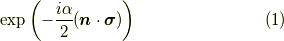
で実現できるかを示します. 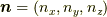 であり,絶対値
であり,絶対値 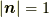 で
で 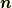 の方向が回転軸の方向です.(右ねじの関係です.)そして,
の方向が回転軸の方向です.(右ねじの関係です.)そして, 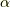 が回転角の大きさです.私の 以前の記事 では,『EMANの物理学』さんの スピノールの記事 を引用しましたが,EMANさんはz軸方向の回転のみをお扱いになっておられたので,他の軸の回転も含めて理由を説明したいと思います.
が回転角の大きさです.私の 以前の記事 では,『EMANの物理学』さんの スピノールの記事 を引用しましたが,EMANさんはz軸方向の回転のみをお扱いになっておられたので,他の軸の回転も含めて理由を説明したいと思います.
無限小回転と有限回転
何らかのパラメータ 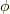 を持った関数
を持った関数 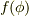 の微小回転は,
の微小回転は,
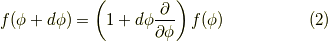
で表現できます.
パラメータ増分 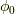 の有限回転にするには,これを
の有限回転にするには,これを 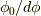 回行い,
回行い, 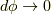 に近づけます.
に近づけます.
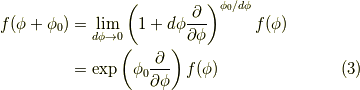
これは後で使います.
任意方向のスピノール
パウリ行列を
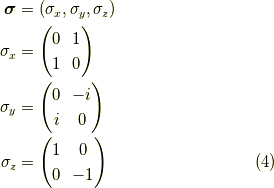
とします.ここで, 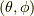 方向を向いたスピノール
方向を向いたスピノール 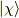 を考えます.
それは,
を考えます.
それは,
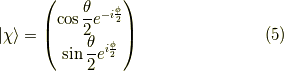
となります.これは,スピノールの向く方向を表す単位ベクトル 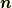 を使った固有値問題,
を使った固有値問題,

の固有スピノールです.
接スピノールを集める(z軸周り)
ここで, 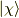 の偏微分を考えます.
の偏微分を考えます. 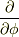 は解釈がしやすいです.
やってみましょう.
は解釈がしやすいです.
やってみましょう.
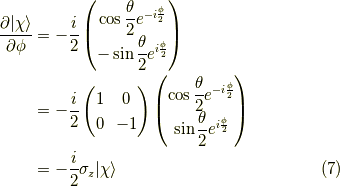
よって,  軸周りの角度
軸周りの角度 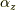 回転は,
回転は,
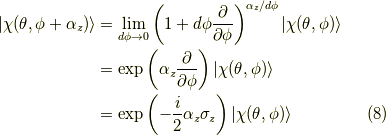
ですから,
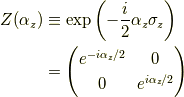
接スピノールを集める(y軸周り)
次に, 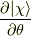 を求めます.
を求めます.
ここで,パラメータを設定しておきます.詳しくは図を見てください.
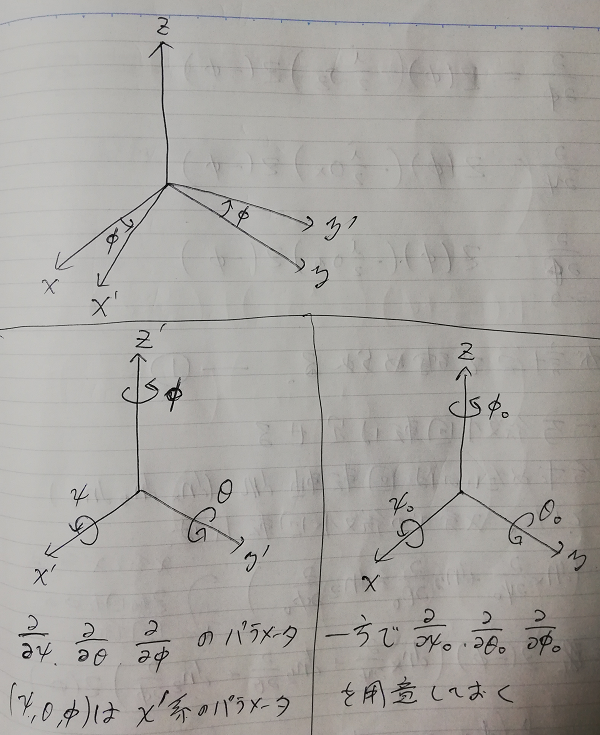
ここで  系は空間の基本的な枠組みでそこでスピノールの向きが指定されます.
一方,
系は空間の基本的な枠組みでそこでスピノールの向きが指定されます.
一方, 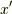 系はスピノールの
系はスピノールの 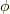 方向を
方向を 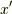 軸に合わせたものです.
つまり,いつスピノールを見ても,
軸に合わせたものです.
つまり,いつスピノールを見ても, 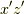 平面にスピノールがあります.
平面にスピノールがあります.
何を意図しているか言ってしまうと,  系は演算
系は演算 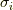 と深い関係があり,
と深い関係があり, 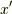 系は
系は 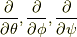 と関係が深いです.
と関係が深いです.
ここで, 複雑な回転を単純な回転で表す方法 を知っていると分かりやすいですが, 一応,こちらで必要な分だけ説明しようと思います.
今, 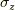 は
は  軸周りの回転
軸周りの回転 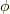 での微分を表すのでした.
同様に,
での微分を表すのでした.
同様に, 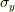 は
は 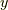 軸周りの回転方向の接スピノールを得る操作と考えられます.
しかし,今回は
軸周りの回転方向の接スピノールを得る操作と考えられます.
しかし,今回は 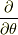 は
は 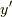 軸周りの回転方向の接スピノールを得る操作を表します.
なぜならば,
軸周りの回転方向の接スピノールを得る操作を表します.
なぜならば, 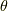 はスピノールの向きを表していて,その向きから
はスピノールの向きを表していて,その向きから 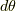 だけ変化する方向を考えるからです.
ここで,以下の操作を考えます.
だけ変化する方向を考えるからです.
ここで,以下の操作を考えます.
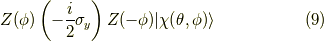
この操作は 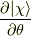 を表しています.
を表しています.
1.まず, 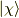 があります.
があります.
2.これを  軸周りに
軸周りに 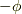 だけ回転させて,
だけ回転させて, 平面内にスピノルを持ってきます.
平面内にスピノルを持ってきます.
3.ここで 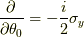 を施し,
を施し, 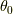 方向の接スピノールを求めます.
方向の接スピノールを求めます.
4.最後に  軸周りに
軸周りに 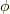 だけ回転させて,
だけ回転させて, 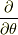 を施した
を施した 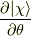 を得ます.
を得ます.
つまり,この一連の操作は, 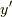 周りの回転
周りの回転 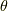 方向への接スピノールを求めたことになります.
方向への接スピノールを求めたことになります.
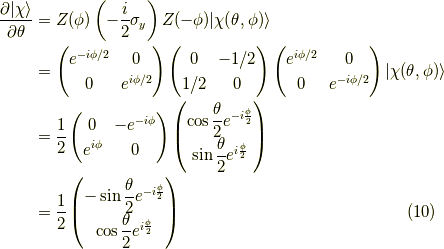
の関係があります.これで, 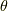 方向の接スピノールも得られました.
方向の接スピノールも得られました.
確認をしておくと,実際,スピノールを微分した結果と比べると,
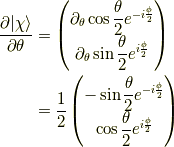
と一致します.
接スピノールを集める(x軸周り)
最後に 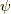 の接スピノールです.これは,最初分かりませんでした.
でも,こう考えればよいです.
の接スピノールです.これは,最初分かりませんでした.
でも,こう考えればよいです.
さっき, 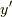 軸周りの回転を表すのに
軸周りの回転を表すのに 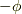 回転させ,
回転させ, 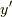 軸を
軸を 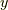 軸にもってきました.
今度は,
軸にもってきました.
今度は, 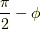 回転させて,
回転させて, 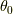 軸周りに
軸周りに 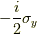 で接スピノールを求め,
最後に
で接スピノールを求め,
最後に 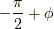 回転させたものが,
回転させたものが, 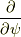 となります.つまり,
となります.つまり, 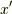 軸周りの回転方向の接スピノールが求まった訳です.
軸周りの回転方向の接スピノールが求まった訳です.
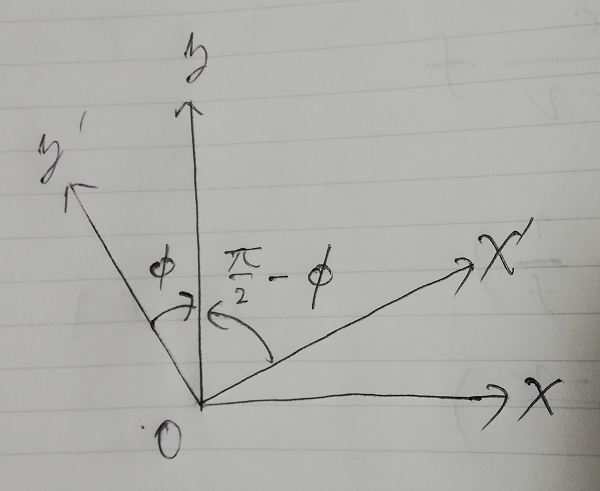
よって,今度は,
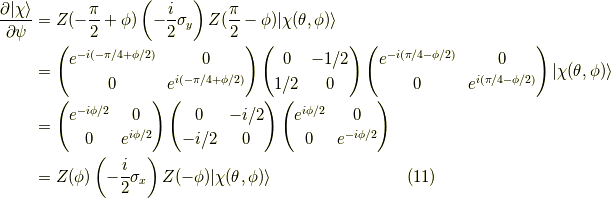
が間接的にではありますが,示せました.
最初の  軸周りの接スピノールも形式を揃えて,リストにすると,
軸周りの接スピノールも形式を揃えて,リストにすると,
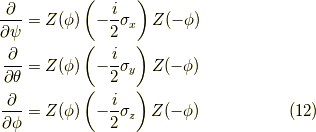
となる訳です.(左辺は一応行列だと思います.スカラーとして 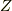 を左辺に移すとスカラーだった場合,
を左辺に移すとスカラーだった場合, 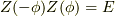 で打ち消されてしまうから,
で打ち消されてしまうから, 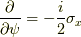 という間違った数式になるからです.ここらへんは難しいです..)
という間違った数式になるからです.ここらへんは難しいです..)
本題
ここで,微小回転 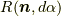 を,回転軸の方向を持つ単位ベクトル
を,回転軸の方向を持つ単位ベクトル 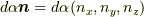 (
( 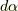 は微小回転角)を用いて表せて,
は微小回転角)を用いて表せて,
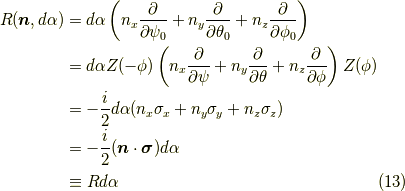
となります.注意として微小回転ならば,有限回転と違って足し合わせるし,可換になります.
後は, 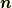 軸周りの微小回転が表現できたので,
軸周りの微小回転が表現できたので,
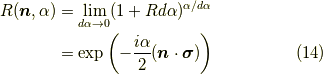
これがスピノールを回転軸 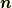 として,その方向を右ねじが進む方向に一致させた回転角
として,その方向を右ねじが進む方向に一致させた回転角 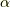 だけ回転させる演算です.
それでは今日はここまで.お疲れ様でした.
だけ回転させる演算です.
それでは今日はここまで.お疲れ様でした.