この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
単純な図形を不変にする滑らかな流れの生成法
この記事では,便利なベクトル場を生成する手法を論じます. 大雑把な話ですが,なかなか興味深いと思います.
いきなりの本題
二次元平面上に2つの連続な陰関数

があるとします.
これは簡単に解釈すると,それぞれ境界で囲まれたある有界な領域から離れるにしたがって, 値を増す関数が左辺で,その等高線を指定するのが右辺の定数値です. もちろん離れるにしたがって負に増大する場合はありますが,ここでは考えません. その場合は全体にマイナスを掛ければいいからです.
ここで,関数 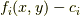 は,それがゼロになる集合で仕切られる
領域の内側と外側では,必ず正のみか,負のみになり,混じることはありません.
なぜなら,混じっているなら,その領域間に境界が存在するはずだからです.
は,それがゼロになる集合で仕切られる
領域の内側と外側では,必ず正のみか,負のみになり,混じることはありません.
なぜなら,混じっているなら,その領域間に境界が存在するはずだからです.
ここで, 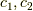 を固定して,動くパラメータ
を固定して,動くパラメータ 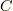 を考えます.
下を考えてみましょう.
を考えます.
下を考えてみましょう.

これって, 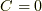 の時は左辺の積の因子
の時は左辺の積の因子 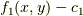 (これをゼロにする曲線を
(これをゼロにする曲線を 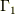 とする)か
とする)か 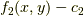 (同じく
(同じく 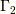 とする)がゼロになっている時で,つまり,式
とする)がゼロになっている時で,つまり,式 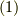 の和集合
の和集合 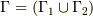 です.
です.
面白いのはここからです. 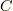 を正負に動かしてみると,
を正負に動かしてみると, 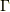 に滑らかに沿った
曲線群になります.ここで,
に滑らかに沿った
曲線群になります.ここで, 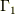 から近い
から近い 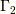 の点を
みると,
の点を
みると, 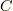 が正になった時,
が正になった時, 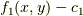 が小さいの
で,
が小さいの
で, 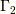 からはある程度離れた点でもある点で,式
からはある程度離れた点でもある点で,式 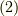 を満たした点の集合を作ります.
一方,
を満たした点の集合を作ります.
一方, 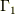 から大きく離れると,
から大きく離れると, 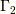 はほとんど元の図形から動きません.
はほとんど元の図形から動きません.
具体例
5つほど,上げておきます.(数式可視化ソフトのdesmosを使うといいです)
(1)双曲線

(2)四直線に沿う曲線群
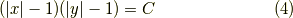
カッシーニの卵型( 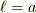 ではレムニスケート)
ではレムニスケート)
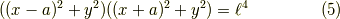
非対称なカッシーニの卵型
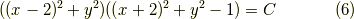
便利なツールとして
これベクトル場で良い感じのを取ってくるのに使えますね. 手計算ではなかなか複雑ですが,数値計算なら有効な手法かと思います.
つまり,曲線の法線ベクトルを求める手法である外微分 (これは一形式なので,それからベクトル場にしたもの)をとったり, それに直交した曲線に沿うベクトルを容易に得ます.(単純な計算とは言っていない)
法線ベクトル場 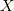 は,
は, 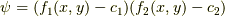 として,
として,
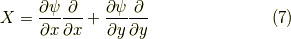
接線ベクトル場 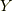 は,
は,
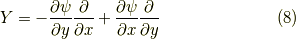
となります.どうです?なかなか便利そうな手法ではありませんか?
今日はここまで.お疲れさまでした.