この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ホッジ作用素を使った公式補足
外積代数に関して重要な事柄は,ここまでの記事でほとんどですが, ホッジ作用素 に関する公式だけ,少し補足しておきます.
ホッジ作用素を二回作用させる
以下の議論では,空間の向きを保つとします.(つまり,右手系⇔左手系を途中で入れ替えません.)さて,一般のウェッジ積の次数に関し, 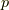 ベクトル
ベクトル 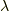 と
と 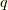 ベクトルのウェッジ積
ベクトルのウェッジ積 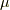 について次の関係がなりたちました.( ウェッジ積について補足 を参照して下さい.)
について次の関係がなりたちました.( ウェッジ積について補足 を参照して下さい.)
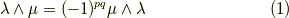
これを基底 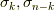 に適用すると次のようになります.ただし,
に適用すると次のようになります.ただし, 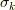 は
は 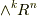 の基底,
の基底, 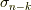 は
は 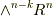 の基底とします.
の基底とします.
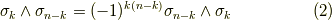
一方,ホッジ作用素の定義式より,次式が言えました.空間の計量が分からないので,右辺の内積はそのままにしておきます.
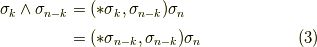
式 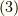 で
で 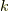 と
と 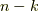 を入れ替えると次式を得ます.
を入れ替えると次式を得ます.
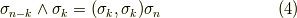
そこで,式 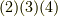 を見比べて,次式が得られます.これは言わば,ホッジ作用素の逆作用を表わす式だと言えます.
を見比べて,次式が得られます.これは言わば,ホッジ作用素の逆作用を表わす式だと言えます.
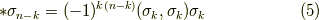
式 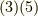 より,ホッジ作用素を二回連続して作用させる場合の表式を得られます.(いま,基底としては正規直交基底を考えていますので,
より,ホッジ作用素を二回連続して作用させる場合の表式を得られます.(いま,基底としては正規直交基底を考えていますので, 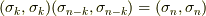 となることに注意して下さい.)
となることに注意して下さい.)
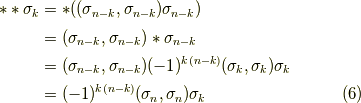
基底の内積 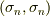 は, p-ベクトルの内積 で定義したように,
は, p-ベクトルの内積 で定義したように, 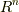 の基底のうち,計量がマイナスとなる基底の個数に応じて
の基底のうち,計量がマイナスとなる基底の個数に応じて 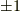 のどちらかの値を取ります.これで,ホッジ作用素を二連続で作用させた場合の公式が得られました.ボリュームフォームの内積は,
のどちらかの値を取ります.これで,ホッジ作用素を二連続で作用させた場合の公式が得られました.ボリュームフォームの内積は, 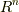 の基底で計量を負をするもの(例えばミンコフスキー空間の時間軸)の個数を
の基底で計量を負をするもの(例えばミンコフスキー空間の時間軸)の個数を  として,
として, 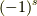 と書けますので,式
と書けますので,式 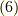 は次のようにまとめられます.(符号定数
は次のようにまとめられます.(符号定数 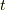 を使って
を使って 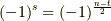 としても同じです.)
としても同じです.)
theorem
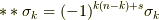
具体例
三次元ユークリッド空間 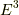 で考えましょう.正規直交基底を
で考えましょう.正規直交基底を 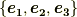 と取り,ボリュームフォームを
と取り,ボリュームフォームを 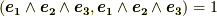 と決めます.このとき,例えば,
と決めます.このとき,例えば, 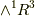 の基底
の基底 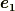 と
と 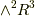 の基底
の基底 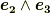 は,ホッジ作用素によって次のように移されるのでした.( ホッジ作用素 の記事の具体例で考えました.)
は,ホッジ作用素によって次のように移されるのでした.( ホッジ作用素 の記事の具体例で考えました.)
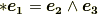
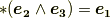
公式 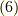 は,確かにこの結果を説明しています.
は,確かにこの結果を説明しています.
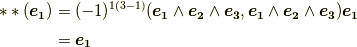
ちゃんと元に戻ってきました(^ ^).
一つの定理
ホッジ作用素に関して,もう一つ定理を補足しておきます. 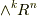 に属する二つの元
に属する二つの元 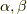 に対し,次式が成り立ちます.
に対し,次式が成り立ちます.
theorem
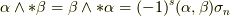
proof
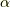 を
を 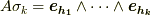 と書くとき,定理の両辺を
と書くとき,定理の両辺を 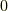 にしないのは,
にしないのは, 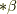 の基底が
の基底が 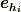 を含まないときだけです.( ホッジ作用素 の記事を参照して下さい.)このことは,裏を返せば
を含まないときだけです.( ホッジ作用素 の記事を参照して下さい.)このことは,裏を返せば 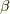 の基底が
の基底が 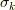 だということです.そこで,
だということです.そこで, 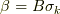 と書きます.
と書きます. 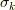 と,構成する基底を重複しない
と,構成する基底を重複しない 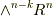 の基底を
の基底を 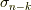 と書きます.このとき,
と書きます.このとき, 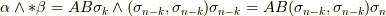 と変形できますが,さらに式
と変形できますが,さらに式 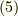 を用いて
を用いて 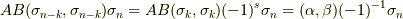 と変形されます.これで定理が示されました.■
と変形されます.これで定理が示されました.■
参考文献
- 著,『 Differential Forms with Applications to the Physical Science』( Dover Publications Inc., 1990, 032111583x)