この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
シュレーディンガー方程式のグリーン関数
この記事では,シュレーディンガー方程式の自由粒子のグリーン関数を求めます.
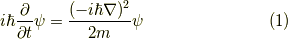
自由粒子のシュレーディンガー方程式の一次元と三次元の形を明示しておくと,

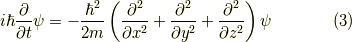
です.
1次元の場合
まず,基本的な一次元空間のシュレーディンガー方程式から考えます. この場合のグリーン関数の定義は,

と言う事にしておきます.右辺の符号はプラスの方が都合がよいです. ここで,フーリエ変換を行います.その定義は,
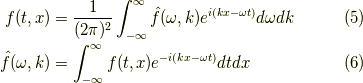
としておきます.
デルタ関数の積分表示,
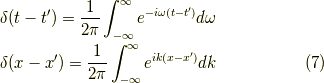
を使います.式 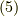 で
で 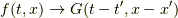 等として,式
等として,式  と共に,式
と共に,式  へ代入すると,
へ代入すると,
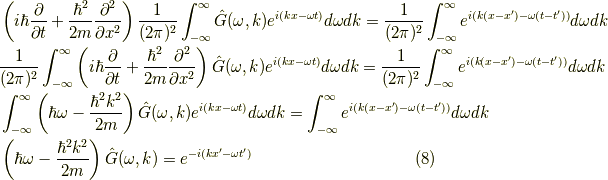
よって,フーリエ変換されたグリーン関数は次の形をしています.
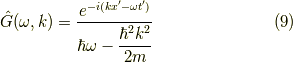
しかし,2点修正が必要です.まず,どういう訳か,式 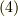 のグリーン関数の右辺は,
のグリーン関数の右辺は, 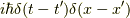 とするのが通例の様です.下に参考文献に上げたファインマンの本でも77ページ,式
とするのが通例の様です.下に参考文献に上げたファインマンの本でも77ページ,式 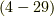 にそうあります.
また,グリーン関数で今回興味があるのは遅延グリーン関数なので,分母に微小な純虚数
にそうあります.
また,グリーン関数で今回興味があるのは遅延グリーン関数なので,分母に微小な純虚数 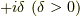 を追加します.そうして,
を追加します.そうして,
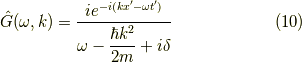
が得られます.これをフーリエ逆変換をして, 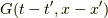 を求めます.
まずは,
を求めます.
まずは, 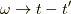 のフーリエ逆変換をします.それは,
のフーリエ逆変換をします.それは,
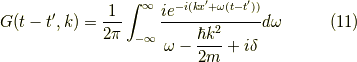
ここで複素関数論の留数定理を用います.  とします.この場合,ジョルダンの補題を
とします.この場合,ジョルダンの補題を  に適用すると,
に適用すると, 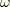 の大きな円弧の積分は下半面でゼロになることが分かります.(佐藤超関数の話だと,極をずらすのではなく実軸上にあるままで,積分路を実軸を含むように
の大きな円弧の積分は下半面でゼロになることが分かります.(佐藤超関数の話だと,極をずらすのではなく実軸上にあるままで,積分路を実軸を含むように 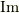 方向に微小距離だけずらすのが正確な方法だそうです.詳しくは こちら )
方向に微小距離だけずらすのが正確な方法だそうです.詳しくは こちら ) 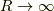 として,図の積分路では
として,図の積分路では 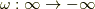 に注意してください.留数を取るときマイナス1が余計に出ます.
に注意してください.留数を取るときマイナス1が余計に出ます.


ここで,ω積分を終えて役目を終えた  の
の 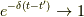 という極限を取りました.
次に
という極限を取りました.
次に 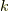 でフーリエ逆変換を行います.
でフーリエ逆変換を行います.
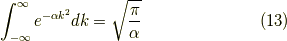
を,行います.(詳しくは 虚数のガウス積分 )
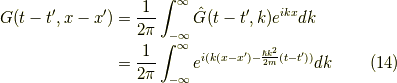
ここで,指数関数の中身を変形します.平方完成です.

二乗の中身は,式 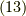 のガウス積分で,実数のずれを無視して,係数の情報のみ残ります.
また,平方完成のおつりは残ります.
のガウス積分で,実数のずれを無視して,係数の情報のみ残ります.
また,平方完成のおつりは残ります.
これで一段落です.
次に  ですが,これは簡単です.
ですが,これは簡単です.  複素数平面で上半面の積分にすると,円弧の積分はゼロになります.一方で,極は
複素数平面で上半面の積分にすると,円弧の積分はゼロになります.一方で,極は 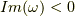 に一つあるだけなので,その積分路は極を含まず上半面で正則です.つまり,
に一つあるだけなので,その積分路は極を含まず上半面で正則です.つまり, 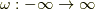 の逆フーリエ変換はゼロになります.よって,一次元の場合のグリーン関数の
の逆フーリエ変換はゼロになります.よって,一次元の場合のグリーン関数の  表示が求まりました.
表示が求まりました.
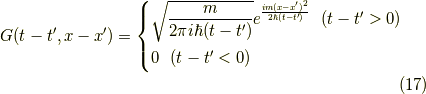
一次元のグリーン関数の解釈
ここで,解の検証です. 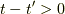 を固定しましょう.
すると,正規分布関数
を固定しましょう.
すると,正規分布関数 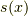 として,
として,

に近いことが分かります. 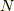 は規格化定数です.分布の中心が
は規格化定数です.分布の中心が 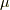 で,広がりの目安(標準偏差)が
で,広がりの目安(標準偏差)が  です.
一方,グリーン関数の指数部分
です.
一方,グリーン関数の指数部分 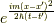 は,
は,
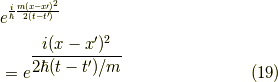
となります.これは,最初に粒子が存在していた点 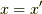 の近傍では複素数値の振動が穏やか(正確には波数が小さい)で,そこから離れるに従って振動が激しくなっていきます.ここで,穏やかな振動の所で最も存在確率が高くなると考えます.(逆に複素数の激しい振動では粒子は存在しないと考えます.数学では「 リーマンルベーグの補題 」と言うようです.)
となると,式
の近傍では複素数値の振動が穏やか(正確には波数が小さい)で,そこから離れるに従って振動が激しくなっていきます.ここで,穏やかな振動の所で最も存在確率が高くなると考えます.(逆に複素数の激しい振動では粒子は存在しないと考えます.数学では「 リーマンルベーグの補題 」と言うようです.)
となると,式  も
も 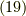 も指数の肩の値の分子が0に近いほど,粒子の存在確率が大きいことになります.
つまり,式
も指数の肩の値の分子が0に近いほど,粒子の存在確率が大きいことになります.
つまり,式 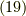 の電子雲の広がりは
の電子雲の広がりは 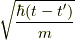 程度であると考えられます.
程度であると考えられます.
また, 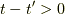 を一つ固定し,
を一つ固定し, 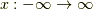 で積分すると,
で積分すると,
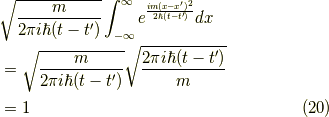
の様に,常に(位相が無く実数で)1です.これは, 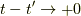 の極限で,デルタ関数になることを意味しています.
の極限で,デルタ関数になることを意味しています.
ここで,波動関数の時間発展を考えてみましょう.  と
と 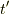 ,
,  と
と 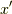 が近い値をとるとします.このグリーン関数は,元々の波動関数の形状を
が近い値をとるとします.このグリーン関数は,元々の波動関数の形状を  とし,その各点の形状の変化をシュレーディンガー方程式に従って追って,最後に重ね合わせたものが,微小時間
とし,その各点の形状の変化をシュレーディンガー方程式に従って追って,最後に重ね合わせたものが,微小時間 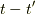 経過した時の波動関数
経過した時の波動関数 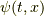 となることが参考文献のp.54,式
となることが参考文献のp.54,式 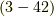 にあります.ここでの文脈に合わせて記号を直して書くと,
にあります.ここでの文脈に合わせて記号を直して書くと,

となります.この積分は畳み込みと呼ばれます. イメージを鮮明に伝える力は僕にはありませんが,つじつまが合うかどうかをチェックする位は出来ます.
例えば,式 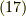 の規格化定数
の規格化定数  も含めると,
も含めると, 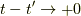 の極限では位相が実数のデルタ関数になることが分かりました.つまり,この極限で畳み込みを考えると,
の極限では位相が実数のデルタ関数になることが分かりました.つまり,この極限で畳み込みを考えると,
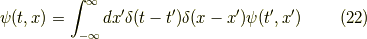
となり,デルタ関数の性質から 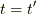 ,
, 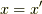 である位相を変えない恒等変換であることが分かります.
では,
である位相を変えない恒等変換であることが分かります.
では,  を増大させていくとどうなるでしょう?式
を増大させていくとどうなるでしょう?式 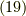 を見ると,全ての点で位相は減っていくことが分かります.
元々の恒等変換で位相は変化していなかったので,そこからの
を見ると,全ての点で位相は減っていくことが分かります.
元々の恒等変換で位相は変化していなかったので,そこからの  の増大ではグリーン関数の畳み込みは位相を減ずる効果があります.さて,平面波
の増大ではグリーン関数の畳み込みは位相を減ずる効果があります.さて,平面波
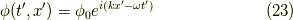
の微小時間後の波動関数 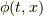 の
の 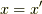 と正(右)の方向に微小距離
と正(右)の方向に微小距離  離れた
離れた 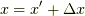 での波動関数は右の方が位相が大きいです.ここで位相を減らすと,高校物理で習ったように波動関数は右に動きます.別の言い方をすると,時間を増大させる場合と似たような効果があると言ってもいいでしょう.
での波動関数は右の方が位相が大きいです.ここで位相を減らすと,高校物理で習ったように波動関数は右に動きます.別の言い方をすると,時間を増大させる場合と似たような効果があると言ってもいいでしょう.
この様に,ある時点での波動関数が分かっていると,その後の時間発展を知ることができるのです.この意味でグリーン関数の事をプロパゲータ(propagate:伝播する)とも言います.フーリエ逆変換で積分核を 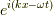 としましたが,
としましたが,  としても,右の方向に進む平面波を表しています.しかし,前者から得られるグリーン関数は前者ではなく,後者に適用すると,波は逆向きに進んでしまいます.その点には気を付けてください.
としても,右の方向に進む平面波を表しています.しかし,前者から得られるグリーン関数は前者ではなく,後者に適用すると,波は逆向きに進んでしまいます.その点には気を付けてください.
老婆心ながら,前者の符号はなぜこうなのかを述べておくと, 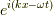 に作用した時,演算子の
に作用した時,演算子の 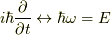 ,
,  の対応を作りたいせいだと思います.
の対応を作りたいせいだと思います.
三次元の場合
最後に三次元の場合に拡張した結果を見ておきましょう.
これは,フビニの定理などで,一次元  の要素を単純に三次元
の要素を単純に三次元  に拡張するだけで良いです.
に拡張するだけで良いです.
つまり,
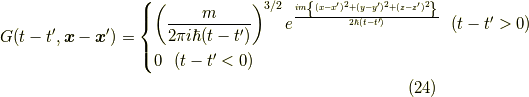
以上で,シュレーディンガー方程式のグリーン関数を求める計算を終わりにします.
今日はここまで,お疲れさまでした!