この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
スピン一重項と三重項のxy方向固有状態での展開
この記事は, 任意の方向を向いたスピンのxyz方向固有状態での展開 という 記事の姉妹編です.
二電子のスピン波動関数のスピンのz成分 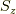 の
固有状態を
の
固有状態を 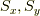 の固有状態で展開してみました.
の固有状態で展開してみました.
S=1,S_z=0の固有状態
波動関数を基底,
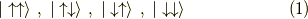
の順番にとります.
これらの線形結合により,z方向のスピン演算子, 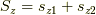 は,
対角化されます.
は,
対角化されます.
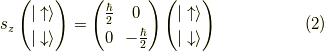
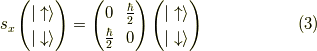
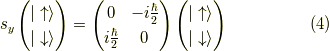
より,
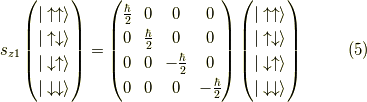
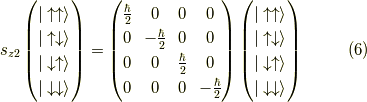

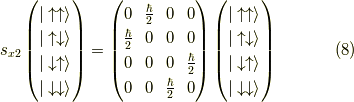
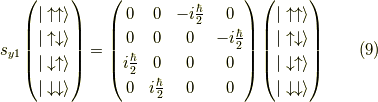
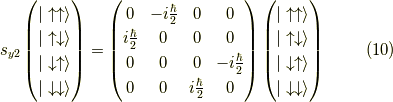
ここで,例えば 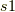 の行列表示は,作用するのは一番目の矢印だけであって,
二番目の矢印を無視して,演算子が一番目の矢印の向きを変える時,
の行列表示は,作用するのは一番目の矢印だけであって,
二番目の矢印を無視して,演算子が一番目の矢印の向きを変える時, 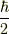 を書き込みます.
以上より,だから,
を書き込みます.
以上より,だから,
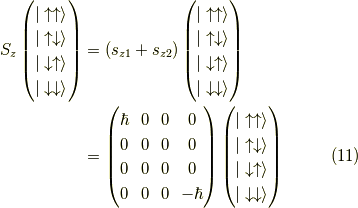
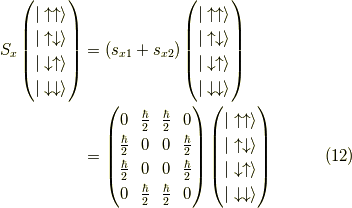
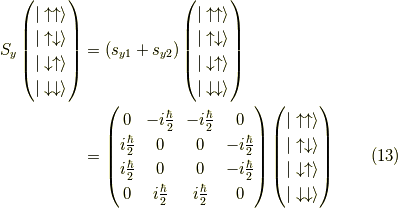
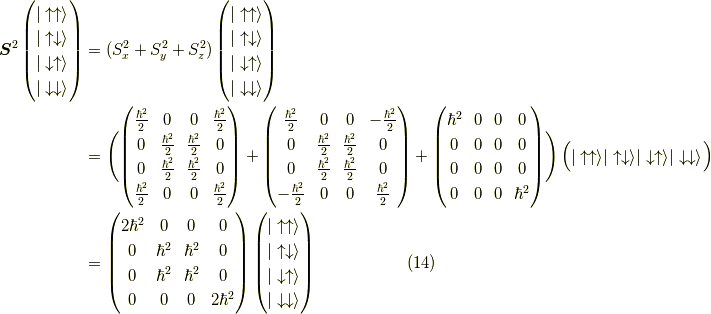
ここで,
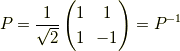
として,式 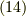 の
の 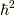 の部分を行列
の部分を行列 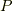 で対角化すると,
で対角化すると,
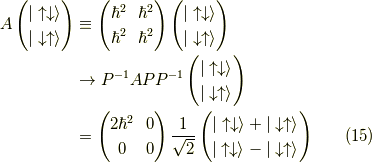
よって, 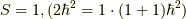 (三重項)
(三重項)

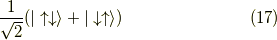

と 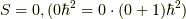 (一重項)
(一重項)
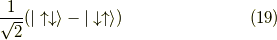
に分かれます.古典的な描像を図にするならば,下図のようになります.

S_x,S_yの固有状態の準備
まずは,固有関数の展開に必要な 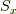 の固有状態を準備します.
以下では簡単のため,
の固有状態を準備します.
以下では簡単のため,
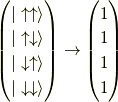
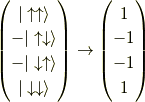
等と書くことにします.
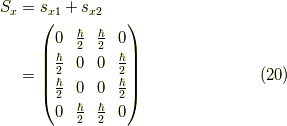
固有値は, 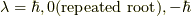 です.(ただし,repeated rootは,重解を表す.)
です.(ただし,repeated rootは,重解を表す.)
固有ベクトルは, 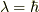 に対し,
に対し,
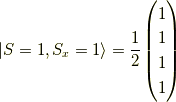
また, 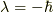 に対し,
に対し,
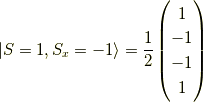
そして, 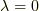 に対し,
に対し,
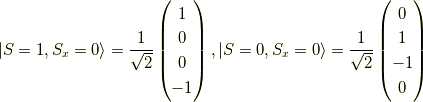
同様に, 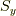 の固有関数を求めると,
の固有関数を求めると,
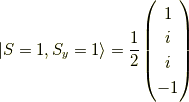
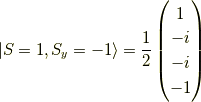
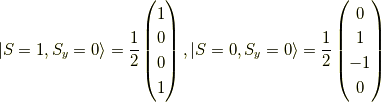
よって, 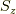 の固有状態を今求めた
の固有状態を今求めた 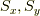 の固有ベクトルで表現すると,
の固有ベクトルで表現すると,
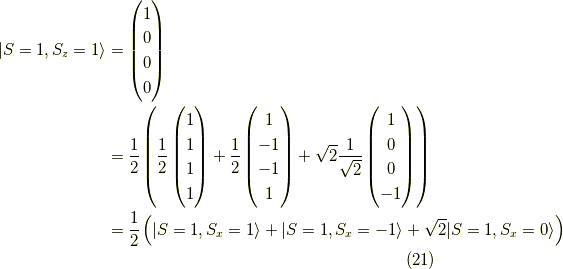
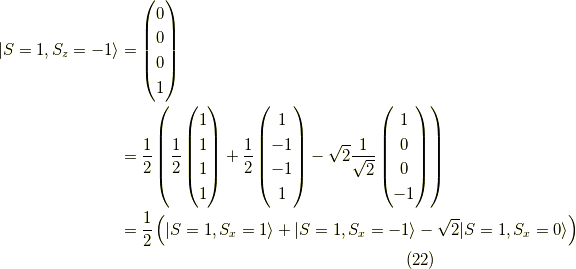
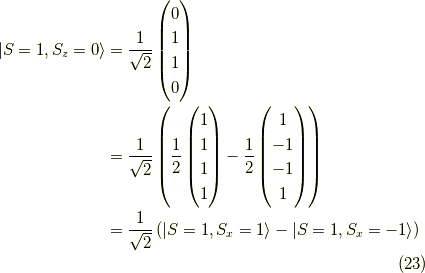
また, 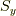 に関しても同様に,
に関しても同様に,
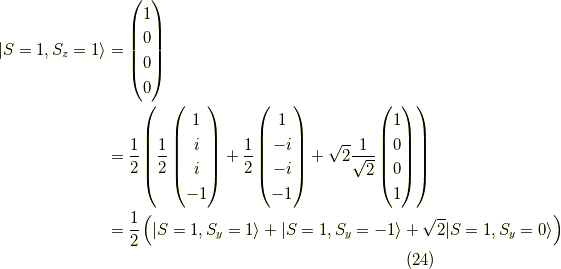
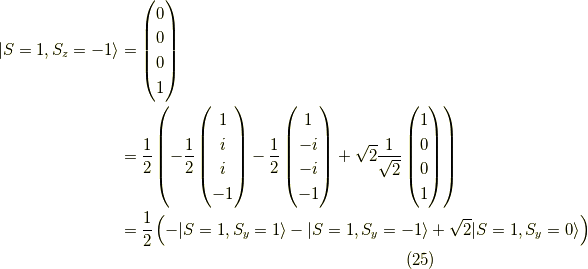
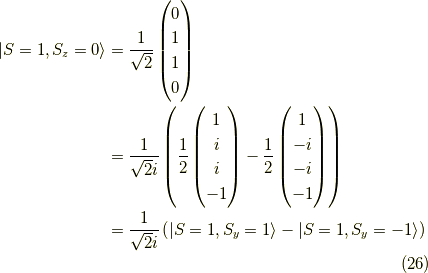
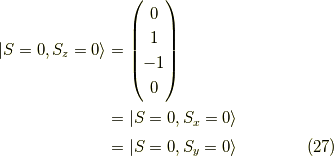
となります.式 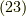 と式
と式 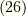 に注目してみましょう.
に注目してみましょう.
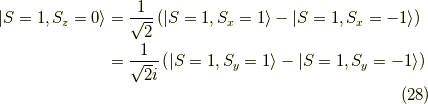
となっていますね. これは,x軸とy軸の周りの回転が, 正と負の両方向の回転が重なっていることを表しています. 古典論では,考えられない状態ですね(^_^;)
それでは,今日はこの辺で.お疲れ様でした^^