この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
スペクトル分解（点スペクトルと連続スペクトル）

スペクトル分解という概念について，話します． 最初に注意しておきますが，かなりおおざっぱな話をします． 今後，分かったら詳細に更新していくつもりです．

点スペクトル

エルミート演算子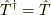（ \hat{T}^\dagger = \hat{T} を満たす）を考えます． その固有状態は直交するのでした．

\hat{T} | \lambda \rangle = \lambda | \lambda \rangle\tag{1}

を考えます．ここで，点スペクトルとは，普通の固有値です．

具体例として，パウリ行列 \sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} の固有値を考えましょう．

\sigma_z | \lambda \rangle = \lambda | \lambda \rangle\tag{2}

固有ベクトルは，

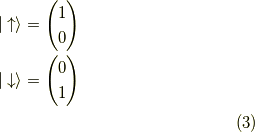
| \uparrow \rangle = \begin{pmatrix}1 \\0\end{pmatrix} \\| \downarrow \rangle = \begin{pmatrix}0 \\1\end{pmatrix} \\\tag{3}

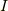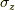ですね．ここでスペクトル分解はこの場合， 恒等演算子 I と \sigma_z とすると，これらは固有ベクトルで分解出来て，

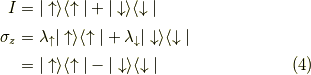
I &= | \uparrow \rangle \langle \uparrow | + | \downarrow \rangle \langle \downarrow | \\\sigma_z &= \lambda_\uparrow | \uparrow \rangle \langle \uparrow | + \lambda_\downarrow | \downarrow \rangle \langle \downarrow | \\&= | \uparrow \rangle \langle \uparrow | - | \downarrow \rangle \langle \downarrow |\tag{4}

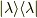となります．この様に，全ての固有値 \lambda に対応するプロジェクション（射影演算子） | \lambda \rangle \langle \lambda | を掛けて足し合わせると，元の演算子を再現できます．

連続スペクトル

この概念はちょっと分かりにくかったです．具体例としては，位置演算子 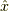\hat{x} を上げましょう．

\hat{x} | x \rangle = x | x \rangle\tag{5}

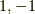これは，どの x に対してもそれに対応した固有ベクトル \langle x | x^\prime \rangle = \delta(x - x^\prime) が存在します．パウリ行列では固有値は 1,-1 でしたから離散的に分布していましたが，この場合，連続的に x が分布しているわけです．

この場合，スペクトル分解は，測度 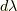d \lambda がちょっとこの書き方で良いか不安ですが，（本当は射影演算子 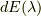dE(\lambda) を使うべき？）

I &= \int d \lambda | x_\lambda \rangle \langle x_\lambda | \\\hat{x} &= \int d \lambda x_\lambda | x_\lambda \rangle \langle x_\lambda |\tag{6}

となります．一個目は見慣れてらっしゃいますかね？ 二個目ちょっと調べておきましょう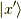． | x^\prime \rangle に演算します．

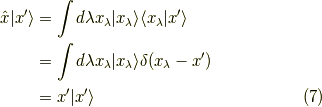
\hat{x}| x^\prime \rangle &= \int d \lambda x_\lambda | x_\lambda \rangle \langle x_\lambda | x^\prime \rangle \\&= \int d \lambda x_\lambda | x_\lambda \rangle \delta( x_\lambda - x^\prime ) \\&= x^\prime | x^\prime \rangle\tag{7}

確かに 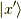| x^\prime \rangle に作用させると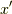， x^\prime を返すのでこれは 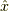\hat{x} と分かります．

有限深さの井戸型ポテンシャル

ここで，両方が混在する話として，有限深さの井戸型ポテンシャルに対するハミルトニアン 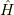\hat{H} を考えます． ポテンシャルを次の様にしておきます．

V(x) = \begin{cases}0 \ \ \ \ (|x| \leq L ) \\V_0 \ \ \ \ (|x| \geq L )\end{cases}\tag{8}

これはご存知の様に，ハミルトニアンの固有値 E=V_0 を境に， その下では束縛状態をなる離散スペクトル（点スペクトル），上では遍歴状態を表す連続スペクトルになります．

この場合のスペクトル分解は，

I &= \sum_i | \psi_i \rangle \langle \psi_i | + \int d \lambda | \psi_\lambda \rangle \langle \psi_\lambda | \\\hat{H} &= \sum_i E_i | \psi_i \rangle \langle \psi_i | + \int d \lambda E_\lambda | \psi_\lambda \rangle \langle \psi_\lambda | \tag{9}

となります．これは，例えば波動関数 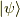| \psi \rangle のエネルギー固有値を求めるのに，

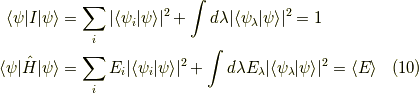
\langle \psi |I| \psi \rangle &= \sum_i | \langle \psi_i | \psi \rangle |^2 + \int d \lambda | \langle \psi_\lambda | \psi \rangle |^2 = 1 \\\langle \psi |\hat{H}| \psi \rangle &= \sum_i E_i | \langle \psi_i | \psi \rangle |^2 + \int d \lambda E_\lambda | \langle \psi_\lambda | \psi \rangle |^2 = \langle E \rangle\tag{10}

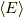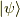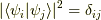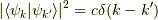となります． \langle E \rangle は状態 | \psi \rangle のエネルギー期待値です．確かに納得される結果ではないでしょうか．離散固有値については | \langle \psi_i | \psi_j \rangle |^2 = \delta_{ij} です．もう一方の連続固有値を考えると，少し波数がずれるとゼロになるでしょうから（なんせ波動関数は無限に広がっているので少しの波数のズレは全体の総和でゼロになる），波数 k などとすると， | \langle \psi_k | \psi_{k^\prime} \rangle |^2 = c \delta(k - k^\prime) の様に振舞いそうです．

最後にグリーン関数

今回の調査で気になったことを最後に書いておきます． 時間依存しないシュレーディンガー方程式は，

\hat{H} | E_i \rangle = E_i | E_i \rangle \tag{11}

となりますね．この場合グリーン関数は，

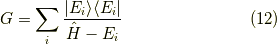
G = \sum_i \dfrac{| E_i \rangle \langle E_i |}{\hat{H}-E_i} \tag{12}

になるんですね．これの確認は，

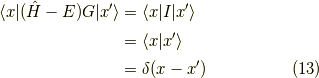
\langle x |(\hat{H}-E) G | x^\prime \rangle &= \langle x | I | x^\prime \rangle \\&= \langle x | x^\prime \rangle \\&= \delta(x-x^\prime)\tag{13}

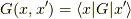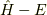となり， G(x,x^\prime) = \langle x | G | x^\prime \rangle を考えると， 確かに演算子 \hat{H}-E を演算させるとデルタ関数になるという意味で， これはグリーン関数です．

結局，今回分かったことは，

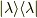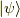エルミート演算子はその固有関数のプロジェクション | \lambda \rangle \langle \lambda | で展開でき， そのプロジェクション自体は幾分抽象的なもので，具体的な考えたい状態 |\psi \rangle で挟むことで確かに元の演算子と同じ振る舞いをすると分かりました．

今日はここまで．お疲れさまでした！