この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
真空中の点源からの電磁場

前フリ

最近，一次元（弦）の波動方程式

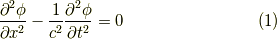
\dfrac{\partial^2 \phi}{\partial x^2}-\dfrac{1}{c^2}\dfrac{\partial^2 \phi}{\partial t^2}=0 \tag{1}

を二次元（膜）にすると，

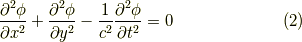
\dfrac{\partial^2 \phi}{\partial x^2}+\dfrac{\partial^2 \phi}{\partial y^2}-\dfrac{1}{c^2}\dfrac{\partial^2 \phi}{\partial t^2}=0 \tag{2}

になる事が分かりました．ということは，ダランベルシアンの値がゼロに等しい方程式は，三次元の振動を表すと推論できます．その方程式は，

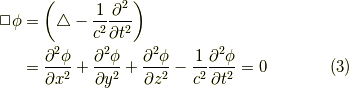
\Box \phi &= \left( \triangle -\dfrac{1}{c^2}\dfrac{\partial^2}{\partial t^2}\right) \\&= \dfrac{\partial^2 \phi}{\partial x^2}+\dfrac{\partial^2 \phi}{\partial y^2}+\dfrac{\partial^2 \phi}{\partial z^2}-\dfrac{1}{c^2}\dfrac{\partial^2 \phi}{\partial t^2}=0 \tag{3}

です．φはポテンシャルです．荷電媒質中の有名な方程式

\Box \phi = -\dfrac{\rho}{\varepsilon} \tag{4}

で電荷の無い真空中（媒質中だと分極が厄介そうです）の時は，上の式で右辺の電荷をゼロにします．ここで，せっかくだからチャージの変化する点電荷（電荷保存則に反するが！）が真空中に作る波動を求めてみました．

解きます！！

当たりをつけて，

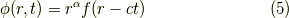
\phi(r,t)= r^\alpha f(r-ct) \tag{5}

としてみました．これのダランベルシアンを取ると，ゼロになることを証明します．まずは式(5)のtでの二階微分これは簡単です．rでの微分を 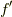f^\prime で表すと，

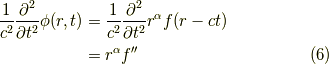
\dfrac{1}{c^2}\dfrac{\partial^2}{\partial t^2}\phi(r,t) &= \dfrac{1}{c^2}\dfrac{\partial^2}{\partial t^2} r^\alpha f(r-ct) \\&= r^\alpha f^{\prime \prime} \tag{6}

今度は，xで一階微分すると，

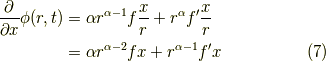
\dfrac{\partial}{\partial x}\phi(r,t) &= \alpha r^{\alpha -1} f \dfrac{x}{r} + r^\alpha f^\prime \dfrac{x}{r} \\&= \alpha r^{\alpha -2} f x + r^{\alpha-1} f^\prime x \tag{7}

xで二階微分すると，

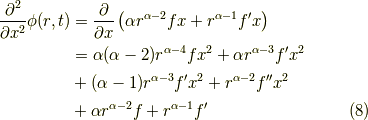
\dfrac{\partial^2}{\partial x^2}\phi(r,t) &= \dfrac{\partial}{\partial x}\left( \alpha r^{\alpha -2} f x + r^{\alpha-1} f^\prime x \right) \\&= \alpha (\alpha - 2)r^{\alpha - 4} f x^2 + \alpha r^{\alpha-3} f^\prime x^2 \\&+ (\alpha-1) r^{\alpha-3} f^\prime x^2 + r^{\alpha -2} f^{\prime \prime} x^2 \\&+ \alpha r^{\alpha -2} f + r^{\alpha -1} f^\prime \tag{8}

よって，これのxをy,zに置き換えれば，ダランベルシアンを取ったものの値は，

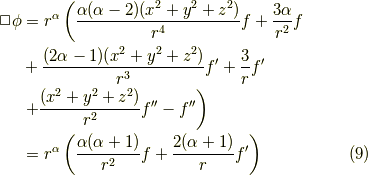
\Box \phi &= r^{\alpha} \left( \dfrac{\alpha(\alpha-2)(x^2+y^2+z^2)}{r^4}f + \dfrac{3 \alpha}{r^2}f \right. \\&+ \dfrac{(2 \alpha -1)(x^2+y^2+z^2)}{r^3} f^{\prime} + \dfrac{3}{r} f^\prime \\&\left. + \dfrac{(x^2+y^2+z^2)}{r^2} f^{\prime \prime} - f^{\prime \prime} \right) \\&= r^{\alpha} \left( \dfrac{\alpha(\alpha+1)}{r^2} f + \dfrac{2(\alpha+1)}{r}f^\prime \right) \tag{9}

よって，これがゼロに等しい時，つまりαが-1の時，これは点電荷から出てくるポテンシャルの波動の解という事になります．

\Box \phi = 0 \tag{10}

の解の一つは，

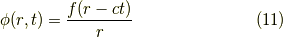
\phi(r,t)= \dfrac{ f(r-ct)}{r} \tag{11}

という事です．ちなみにこれで時間変化しない時，つまり 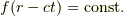f(r-ct)=\mathrm{const.} の時は，このポテンシャルはクーロンポテンシャルになります．今日はここまで，お疲れ様でした．