この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
グリーン関数と逆行列
グリーン関数と逆行列の類似性について書きます.
グリーン関数
演算子 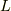 (ただし
(ただし 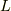 は,
は,  についての演算子)
と既知関数
についての演算子)
と既知関数 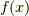 ,未知関数
,未知関数 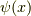 があり以下の関係を満たすとします.
があり以下の関係を満たすとします.

ここで,グリーン関数 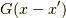 を
次の性質を持つ関数として,
定義します [*] .
を
次の性質を持つ関数として,
定義します [*] .
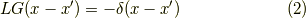
| [*] | その求め方はここでは書きません.普通の演算子 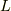 に対してそんな関数が存在するということだけを知っておいてください. に対してそんな関数が存在するということだけを知っておいてください. |
これを使って,形式的に次のように書きます.
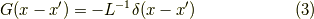
すると,結局未知関数 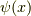 は次のように求まります.
は次のように求まります.
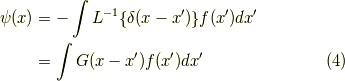
ここで,式 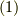 を確認しておきましょう.
式
を確認しておきましょう.
式 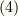 の両辺に
の両辺に 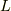 を作用させます.
すると,
を作用させます.
すると, 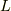 は
は  のみに関わるので,
のみに関わるので,
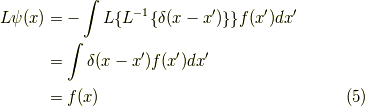
となり,確かに式 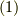 が成立していることが分かります.
が成立していることが分かります.
逆行列
一方,有限次元の逆行列を持つ行列 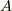 ,
既知ベクトル
,
既知ベクトル 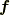 ,
未知ベクトル
,
未知ベクトル 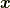 について,
次のような方程式を考えます.
について,
次のような方程式を考えます.

ここで,グリーン関数の行列版とでも言えるような,
次のベクトル群 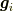 を導入します.
を導入します.
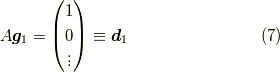
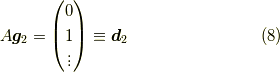
すると,

ですから,
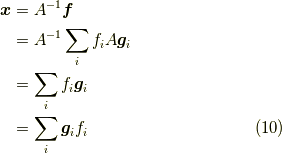
と表せます.ここで, 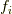 はベクトル
はベクトル 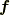 の第
の第 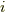 成分
です.
ここで,比較のため,式
成分
です.
ここで,比較のため,式 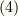 をもう一度書きます.
をもう一度書きます.
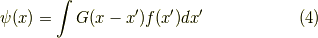
きれいに二つが対応しているのが見てとれますね.
というのは,つまり,δ関数 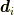 に逆作用素(逆行列)
に逆作用素(逆行列) 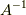 を掛けると,
グリーン関数
を掛けると,
グリーン関数 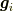 になります.一方,非斉次項の
になります.一方,非斉次項の 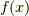 に対応するのが,
に対応するのが, 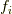 なわけです.
なわけです.
それでは,今日はこの辺で.