この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
電束と電束線

電束と電束線の概念について説明します．

電束とは

ある曲面 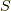S において，電束密度 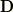\textbf{D} が与えられているとき，

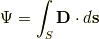
\Psi = \int _S \textbf{D}\cdot d\textbf{s}

で求まる量 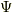\Psi を電束といいます [*] ．簡単に言ってしまえば，電束密度に面積をかけたものが（面積分したものが），その面積を貫く電束，という事になりますね．逆に言えば，単位面積当たりを貫く電束が電束密度という事になります．

[*]この積分の意味については，「ガウスの法則-積分形」を読んでみてください．

また，電束密度の単位は \rm{[C/m^2]} ,電束の単位は \rm{[C]} となります．

電束線とは

電束に対して，電束線というものを考えることが出来ます．

電束密度 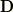\textbf{D} はベクトル量ですよね．このベクトル量を元に，接線の方向が常に 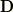\textbf{D} と等しくなるような曲線を書くことが出来ます．この線のことを 電束線 といいます．

また，「線」といった場合には太さのない糸の様なものを思い浮かべることが出来ますが，これに対して電束線を太さのあるホースのようなものに置き換えたものを 電束管 と呼びます．電束線を中心として，小さな半径を持たせたチューブのようなものです．

何に使うの？

電束線の本数を電束密度や電束の大きさに対応させて作図することが出来ます．例えば，電束 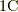1\rm{C} あたりに1本，といった具合です．

この電束線を使うと，本来視覚的に表現するのが難しい電束密度や電束を視覚的に表現することが出来ます．

具体的に見てみましょう電束 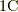1\rm{C} あたりに電束線1本作図することとし，赤，青の点それぞれに 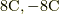8\rm{C},-8\rm{C} の点電荷があるとします．本当は3次元なので，3次元において等方的に8本の電束線が出ていなければなりませんが，3次元で描くのは難しいため，2次元で描くと，次の図のようになります．

shino-DielectricFluxFig1.png shino-DielectricFluxFig2.png

この図において，赤色の点からはそれぞれ8本の電束線が出ていることになります．つまり，点電荷から出てくる電束は全部で 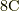8\rm{C} という事になります．これは点電荷の電荷 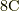8\rm{C} と一致する値ですね．なぜ一致するのかは，ガウスの法則を勉強してみてください．

電束線の性質

電束線にはいくつかの性質があります．それは，

  • 正電荷から始まり，負電荷で終わる
  • 電荷がないところでは，新たに生まれたり消えたりしない
  • 電荷がないところでは，交わったり別れたりすることはない
  • 電束線が込み合っているところでは，電束密度の大きさが大きい
  • 等方的な空間内では，電気力線と一致する [†]
[†]どの方向を向いても同じように見える空間のことを等方的と呼びます．真空中は等方的ですね． しかし，結晶中においては，x方向とy方向の結晶の並びが違ったりするため，方向により電気感受率が違い，等方的でないのが一般的です．

電束線って物理量なの？

電束は 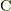\rm{C} という単位を持った単位を持った物理量ですが，電束線は同様に物理量と呼ぶことが出来るのでしょうか？

結論から言ってしまえば，電束線は物理量ではありません．

今の場合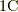， 1\rm{C} あたりに1本と置きましたが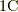， 1\rm{C} あたりに10本とか，0.1本といったようにと置くことも出来ます． 人によって，その値を自由に決めることが出来るため，具体的な数値を決めることが出来ず，物理量と呼ぶことは出来ません．

しかし，物理量ではないからといって全く無意味なものではなく，電磁気学を理解するうえでの 概念 として，非常に有効なものです．

実際に見たり触ったり観測することは出来ませんが，上の図で見たように，電束線を描くことによって，電束密度や電束を容易に，具体的にイメージすることが出来，物理的なイメージを持つための手段として，非常に有効なことが分かりますね．

まとめ

電束とは，電束密度を面積分したもので，その単位は \rm{[C]} です．

電束線とは，その接線が電束密度と一致するような曲線のことで，これを用いると電束や電束密度がどのようになっているかがイメージしやすくなります． また，電束線は上であげたような性質を持ちます．