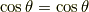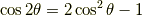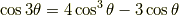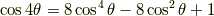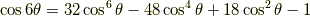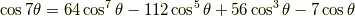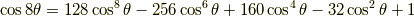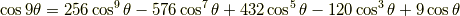この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
三角関数のｎ倍角の公式

三角関数のｎ倍角の公式をひたすら求めてみました． なにかの役に立てば幸いです．

求める方法

行列を使う方法，複素数を使う方法，加法定理を使う方法等がありますが， 今回は，複素数を使う方法で求めました．

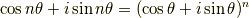
\cos n \theta + i \sin n \theta =(\cos \theta + i \sin \theta)^n

を使います．計算過程は省略します．計算の確認は，表計算ソフトexcelで行いました．

正弦関数の倍角公式

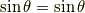
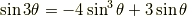
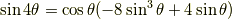
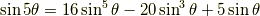
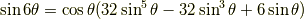
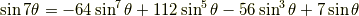
\sin \theta = \sin \theta \sin 2 \theta = \cos \theta (2 \sin \theta) \sin 3 \theta = -4 \sin^3 \theta + 3 \sin \theta \sin 4 \theta = \cos \theta (-8 \sin^3 \theta + 4 \sin \theta) \sin 5 \theta = 16 \sin^5 \theta - 20 \sin^3 \theta + 5 \sin \theta \sin 6 \theta = \cos \theta (32 \sin^5 \theta -32 \sin^3 \theta + 6 \sin \theta) \sin 7 \theta = -64 \sin^7 \theta + 112 \sin^5 \theta -56 \sin^3 \theta + 7 \sin \theta \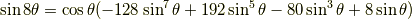sin 8 \theta = \cos \theta (-128 \sin^7 \theta + 192 \sin^5 \theta - 80 \sin^3 \theta + 8 \sin \theta) \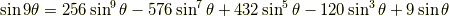sin 9 \theta = 256 \sin^9 \theta - 576 \sin^7 \theta + 432 \sin^5 \theta -120 \sin^3 \theta + 9 \sin \theta \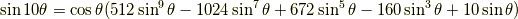sin 10 \theta = \cos \theta (512 \sin^9 \theta -1024 \sin^7 \theta + 672 \sin^5 \theta - 160 \sin^3 \theta + 10 \sin \theta)

余弦関数の倍角公式

\cos \theta = \cos \theta \cos 2 \theta = 2 \cos^2 \theta - 1 \cos 3 \theta = 4 \cos^3 \theta - 3 \cos \theta \cos 4 \theta = 8 \cos^4 \theta - 8 \cos^2 \theta + 1 \cos 5 \theta = 16 \cos^5 \theta - 20 \cos^3 \theta + 5 \cos \theta \cos 6 \theta = 32 \cos^6 \theta -48 \cos^4 \theta + 18 \cos^2 \theta - 1 \cos 7 \theta = 64 \cos^7 \theta - 112 \cos^5 \theta + 56 \cos^3 \theta -7 \cos \theta \cos 8 \theta = 128 \cos^8 \theta -256 \cos^6 \theta + 160 \cos^4 \theta -32 \cos^2 \theta + 1 \cos 9 \theta = 256 \cos^9 \theta -576 \cos^7 \theta + 432 \cos^5 \theta - 120 \cos^3 \theta + 9 \cos \theta \cos 10 \theta = 512 \cos^{10} \theta -1280 \cos^8 \theta + 1120 \cos^6 \theta - 400 \cos^4 \theta + 50 \cos^2 \theta - 1