この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ガロア拡大とガロア群
この記事と次の ガロア群の例 では, 体の自己同型写像 で勉強したガロア拡大とガロア群について,もう少し理解を深めることを目的とします.目新しい概念は出てきませんが,役に立つ定理を幾つか考えます.また,ここまでに既習の事柄も,このあたりで一度頭の整理をしてみて下さい.
ガロア群
ガロア群の元を求める際に,次の定理が便利です.
Important
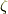 を
を 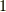 の素数乗根
の素数乗根 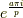 (
( 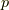 は素数)とします.有理数体
は素数)とします.有理数体 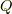 に
に 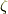 を添加してできる拡大体
を添加してできる拡大体  に対し,ガロア群は整数の剰余群と同型となり,
に対し,ガロア群は整数の剰余群と同型となり, 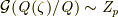 がなりたちます
がなりたちます
proof
いま 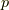 は素数としていますので,剰余群
は素数としていますので,剰余群 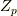 は
は 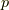 次の巡回群
次の巡回群 ![\{ [0],[1],...,[p-1]\}](http://hooktail.maxwell.jp/kagi/912902578308136e6962fe508b45cd23.png) になります.
になります. 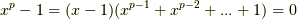 を考えると,
を考えると, 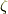 は
は 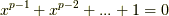 の解ですが,この方程式は
の解ですが,この方程式は 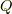 上既約で,
上既約で, 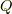 上には解を持たず,体
上には解を持たず,体  は
は 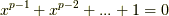 の最小分解体
の最小分解体 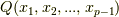 になっており,拡大次数は
になっており,拡大次数は 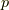 です.よって定理が成り立ちます.■
です.よって定理が成り立ちます.■
例1
有理数体 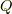 に,
に, 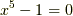 の解の一つである
の解の一つである 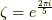 を添加して作った拡大体
を添加して作った拡大体  はガロア拡大になっています.
はガロア拡大になっています.  の元は
の元は  の形をしており,拡大次数は
の形をしており,拡大次数は 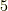 です.一方,ガロア群
です.一方,ガロア群 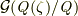 は,
は,  に同型ですので位数は
に同型ですので位数は 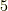 です.よって,
です.よって,  は
は 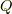 のガロア拡大になっています.
のガロア拡大になっています.
| [*] | 前定理より,拡大次数が 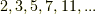 の代数的拡大体は,全てガロア拡大だと言えます. の代数的拡大体は,全てガロア拡大だと言えます. |
ガロア拡大とガロア群に関しては,体の拡大次数が,ガロア群の位数で表されてしまうわけです.とても美しい関係です.
ガロア拡大の別の定義
ここまでに,ガロア拡大とは『 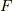 の拡大体
の拡大体  が,
が,  の
の 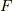 上自己同型写像群
上自己同型写像群 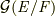 が
が  を固定体とし,
を固定体とし, ![[F:E]=|\cal G \it (E/F)|](http://hooktail.maxwell.jp/kagi/546b41e36aa5aed0fe3bc697f140845b.png) の場合』と定義しました.この定義は分かりやすいものですが,全く同値な定義に言い換えることも出来ます.
の場合』と定義しました.この定義は分かりやすいものですが,全く同値な定義に言い換えることも出来ます.
【ガロア拡大の定義】
![[E:F]=|\cal G \it (E/F)|](http://hooktail.maxwell.jp/kagi/c5bdd334f4b6b2acfdada2979ac1fa56.png)
 は
は  の有限次分離正規拡大体です.
の有限次分離正規拡大体です. は,
は,  上のある分離多項式
上のある分離多項式 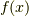 の最小分解体になっています.
の最小分解体になっています.
これらが同値な条件であることは,以下に証明します.場合に応じて,分かりやすい定義を使えば良いと思います.二番目の定義を最初に挙げる教科書が多いようです. 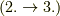 の証明は 体の元の共役と正規拡大体 で示してありますので,ここでは
の証明は 体の元の共役と正規拡大体 で示してありますので,ここでは 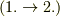 の証明を示します.
の証明を示します.
proof
( 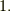 ⇒
⇒ 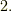 )
)  の任意の元
の任意の元 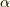 に対し,
に対し, 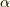 の最小多項式が重解を持たず,かつ
の最小多項式が重解を持たず,かつ  上で一次式の積に分解できることを示せばよいわけです.
上で一次式の積に分解できることを示せばよいわけです. 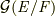 は有限群ですので,
は有限群ですので, 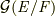 の元の中で相異なるものを集めた集合
の元の中で相異なるものを集めた集合  を考えます
を考えます 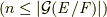 .
.  の任意の元
の任意の元 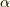 にたいし,この集合の元による写像を
にたいし,この集合の元による写像を  と書き,多項式
と書き,多項式  を考えます.まず各
を考えます.まず各 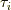 は全て異なるので,
は全て異なるので, 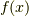 は重解を持ちません.また,
は重解を持ちません.また, 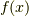 を展開した際の係数は全て
を展開した際の係数は全て 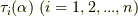 の和と積で表現されますが,これらは固定体
の和と積で表現されますが,これらは固定体 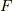 の元になっているはずです.これより,
の元になっているはずです.これより, 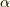 の
の 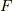 上の最小多項式
上の最小多項式 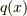 (
( 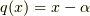 とは限りません)は
とは限りません)は 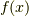 を割るので,
を割るので, 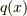 は重解を持ちません.よって
は重解を持ちません.よって 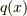 は
は  上一次式の積に分解できます.これより,
上一次式の積に分解できます.これより,  は
は 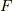 の分離正規拡大体になっています.■
の分離正規拡大体になっています.■
ガロア拡大の表現には,他にも色々なものがあり,教科書によって取り上げ方が様々だと思います.例えば,次の二つの条件が成り立つことも,  が
が 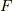 のガロア拡大であることと同値であることを示すことが出来ます.
のガロア拡大であることと同値であることを示すことが出来ます.
【補足】
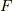 上既約な
上既約な  次方程式
次方程式 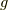 が,もし一つでも
が,もし一つでも  上に解を持てば,
上に解を持てば, 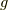 は結局
は結局  個の解を
個の解を  上に持ちます.
上に持ちます. は
は 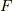 の代数的単純拡大体として表現できます.(つまり,
の代数的単純拡大体として表現できます.(つまり, 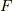 上にある代数的元
上にある代数的元 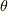 があって,
があって, 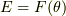 と書けるということ.)
と書けるということ.)
後で使う都合上, 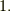 だけ,簡単に証明しておきます.あまり,証明の細かいところにはまらずに,結果だけ了承して先に進んでも良いと思います.
だけ,簡単に証明しておきます.あまり,証明の細かいところにはまらずに,結果だけ了承して先に進んでも良いと思います.
proof
まず必要条件を証明します.  が
が 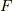 のガロア拡大だとすれば,ガロア群を
のガロア拡大だとすれば,ガロア群を 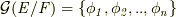 のように決めることができ,
のように決めることができ, 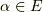 に対し
に対し 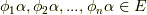 が言えます.これらの中から,
が言えます.これらの中から, 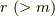 個を選んで,多項式
個を選んで,多項式 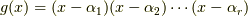 を作ると,
を作ると, 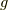 の係数は
の係数は 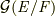 によって動かされませんから(ガロア群の元は
によって動かされませんから(ガロア群の元は 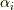 を置換するだけなので),
を置換するだけなので), 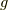 は
は 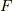 上の多項式だいうことが出来ます.ここで
上の多項式だいうことが出来ます.ここで 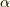 を解とする
を解とする 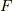 上既約な多項式
上既約な多項式  を考えると(
を考えると(  次多項式とします),
次多項式とします), 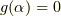 より,
より,  は
は 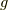 を割るはずですが,
を割るはずですが, 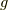 の最小分解体が
の最小分解体が  なので,
なので,  の最小分解体も
の最小分解体も  になり,既約という仮定より,
になり,既約という仮定より,  の解は全て異なるはずです.■
の解は全て異なるはずです.■
proof
次に十分条件を示します. 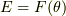 と書け,
と書け, ![[E:F]=n](http://hooktail.maxwell.jp/kagi/db680c7e479d9e83b48e7b21b9db932c.png) とします.いま,
とします.いま,  の最小分解多項式は
の最小分解多項式は  個の解持つはずですので,それを
個の解持つはずですので,それを  とすると,拡大体
とすると,拡大体 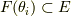 は,全てのの
は,全てのの 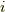 に対して
に対して ![[F(\theta _{i}):F]=n](http://hooktail.maxwell.jp/kagi/86b0b25a982bddc60382b299cfe1f0ba.png) を満たし,結局
を満たし,結局  が言えます.ここで,写像
が言えます.ここで,写像 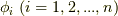 を
を 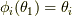 と定義すると,
と定義すると, 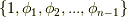 は
は  を
を 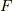 上のベクトル空間とみたときの基底になっており,
上のベクトル空間とみたときの基底になっており, 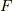 上の多項式
上の多項式 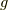 に対して
に対して 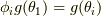 が成り立ちます.これより,
が成り立ちます.これより, 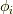 は
は 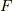 を固定体とする
を固定体とする  の自己同型写像だということが出来て,
の自己同型写像だということが出来て,  は
は 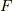 のガロア拡大だと言えます.■
のガロア拡大だと言えます.■
例2
は
のガロア拡大ではありません.
の任意の元は
の形に書けますが,
の共役元である
(
は
の三乗根で
とします)を含まないため,正規拡大にはなっていないからです.
アーベル拡大体と巡回拡大体
特に,ガロア群が可換群である場合のガロア拡大体を アーベル拡大体 ,ガロア群が巡回群である場合のガロア拡大体を 巡回拡大体 と呼びます.