この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
凸関数の性質
熱力学や解析力学で重要となるLegendre変換への準備です.Legendre変換は凸関数や凹関数に対して定義される変換で,その凸性を 保存します.
一変数の凸関数
一変数の凸関数の定義から凸関数の様々な性質を見ていきたいと思います.ちなみに,ここで証明するほとんどの性質は適当な一般化 のもとで多変数の場合にも成り立ちます.
実数上の適当な閉区間 ![[a,b]](http://hooktail.maxwell.jp/kagi/ca400ab3f30b1ab90106538b85afbd2e.png) で定義された下に凸な関数
で定義された下に凸な関数  を考えます.下に凸であることの定義は任意の
を考えます.下に凸であることの定義は任意の ![x,y\in [a,b]](http://hooktail.maxwell.jp/kagi/c50e7c332a5d6551badb2bc24db0a3ef.png) と
任意の
と
任意の  に対して
に対して
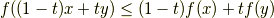
が成り立つことです.ここでこの式の不等号が 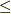 ではなく,
ではなく, 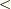 となるようなものを真に下に凸な関数や狭義凸関数などと
言うことがあります.また,不等号が反対の不等式を満たす関数を上に凸な関数とか凹関数などと言います.
となるようなものを真に下に凸な関数や狭義凸関数などと
言うことがあります.また,不等号が反対の不等式を満たす関数を上に凸な関数とか凹関数などと言います.  が
上に凸なら
が
上に凸なら 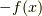 は下に凸ですから,以下は下に凸な関数の場合だけを考えていくことにしましょう.
は下に凸ですから,以下は下に凸な関数の場合だけを考えていくことにしましょう.
まず,凸関数の大切な性質をあげておきます.
1.閉区間 ![[a,b]](http://hooktail.maxwell.jp/kagi/ca400ab3f30b1ab90106538b85afbd2e.png) 上の凸関数は開区間
上の凸関数は開区間 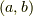 上Lipschitz連続である.よって,凸関数は開区間
上Lipschitz連続である.よって,凸関数は開区間 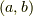 上連続関数である.
上連続関数である.
2.閉区間 ![[a,b]](http://hooktail.maxwell.jp/kagi/ca400ab3f30b1ab90106538b85afbd2e.png) 上の凸関数は開区間
上の凸関数は開区間 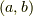 上の任意の点
上の任意の点  で,右側微係数と左側微係数を持つ.つまり,任意の
で,右側微係数と左側微係数を持つ.つまり,任意の 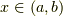 に対して
に対して
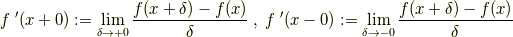
が存在する.
3.ここで,右側微係数と左側微係数に関して次の性質が成り立つ.  として,
として,

がなりたつ.
以上の性質は,グラフを見てみたらとても分かりやすい結果ですね.ここでは,いずれも解析的に証明してみることにします. まず,次のセクションで上の証明に非常に便利な不等式を得ることにします.
凸関数の基本的な不等式
それでは,(1)-(3)の性質を証明するときにとてもお世話になる不等式を証明しましょう.  は
は  で下に
凸な関数であるとします.
で下に
凸な関数であるとします.
任意の  に対して,
に対して,  の凸性より任意の
の凸性より任意の  に対して
に対して

が成り立ちます.(両辺から  を引いて,
を引いて, 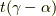 で割ればよいです.)真に下に凸な関数については等号は不成立です.
で割ればよいです.)真に下に凸な関数については等号は不成立です.
ここで, 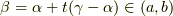 と置いて,
と置いて,
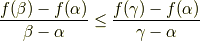
を得ます.同様にして, ![\alpha<\beta<\gamma\in[a,b]](http://hooktail.maxwell.jp/kagi/0cb0accee63bd943756c967d1bb33ef0.png) に対して
に対して  が下に凸ならば次の不等式
が下に凸ならば次の不等式
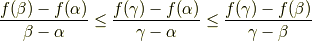
が成り立ちます.これで証明の準備が整いましたから,次のセクションから証明をしていきましょう.
凸関数の性質(1),(2),(3)の証明
さて,(1),(2),(3)の関係を証明してしまいましょう.
(1)前のセクションで示した不等式から,
任意の 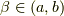 をむ閉区間
をむ閉区間 ![[\alpha,\gamma]](http://hooktail.maxwell.jp/kagi/e7387758d9b5f6259d25b692cfab53ff.png) に対して
に対して ![\forall x\in [\alpha,\gamma]](http://hooktail.maxwell.jp/kagi/fccc9d0900536c46b884a2a723ce05c2.png) に対して,不等式
に対して,不等式
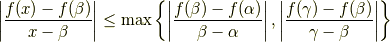
が成り立ちます.よって,
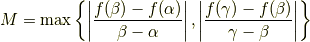
と置けば,
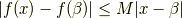
となります.つまり,凸関数はLipschitz連続であることが分かりましたから連続関数です.
(2)さらに, ![\beta\not =x\in [\alpha,\gamma]](http://hooktail.maxwell.jp/kagi/d19b4b281058ecc638ba260819d86478.png) に対して,
に対して, 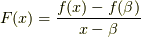 と置けば,
不等式
と置けば,
不等式 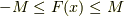 が成り立ちます.
が成り立ちます. 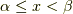 で
で 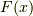 は単調に
増加して,
は単調に
増加して, 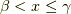 でも
でも 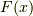 は単調に増加します.ゆえに,
は単調に増加します.ゆえに, 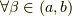 に対して,
左極限と右極限
に対して,
左極限と右極限
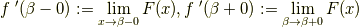
がそれぞれ存在することがわかります.(有界な単調関数の極限が存在することを使っています.)
(3)さらに,前のセクションで示した不等式と上の結果を合わせて,次の二つの不等式が分かります. 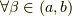 に対して
に対して
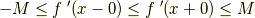
が成り立ちます.なお,真ん中の不等式の等号成立条件は  が
が  を含むある区間で微分可能であることが必要十分です.
を含むある区間で微分可能であることが必要十分です.
また ![\forall \alpha<\forall \beta\in [a,b]](http://hooktail.maxwell.jp/kagi/31f73dbe25f2cec04d1dc642a8f3a824.png) に対して
に対して
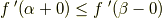
です.等号成立条件は  が区間
が区間 ![[\alpha,\beta]](http://hooktail.maxwell.jp/kagi/2aaaf5839259231e54ae05081f3a2b0f.png) で線形であることです.
で線形であることです.