この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ミラー指数(面)
結晶は単位格子が集まったものですが,原子で作られる面の集まりとみることもできます. 結晶の外形に特定の結晶面が現れることもよくあります. 実際の結晶では互いに平行で等間隔の距離で並んでいる結晶面が無数にならんでいるのです.
このような1組の面の集合を結晶格子面といいます.
結晶ではこんな結晶格子面がたくさんあります.
これを表したいときに使うのがミラー指数(Miller index)です.
ミラー指数は 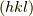 というふうに,「丸括弧の中の3つの整数」で表示し,
それによって任意の格子面を表現することができます.
ここでは,任意の格子面をミラー指数で表現する手続きを紹介します.
というふうに,「丸括弧の中の3つの整数」で表示し,
それによって任意の格子面を表現することができます.
ここでは,任意の格子面をミラー指数で表現する手続きを紹介します.
面のミラー指数を得る手順
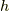 は
は  軸,
軸, 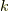 は
は  軸,
軸, 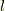 は
は  軸とそれぞれ対応しています.
軸とそれぞれ対応しています.
手順 1
単位格子の3つの主軸を座標軸にとります.

この図はすべての軸が直交していますが, 単位格子が歪んでいたら座標軸も歪みます.
手順 2
それぞれの座標軸に,それぞれの単位格子の 辺の長さ(格子定数)を単位として目盛りを打ちます.

手順 3
表したい格子面がこの3つの座標軸を切る交点の位置を, 先ほど打った目盛りの単位で表します. このとき,格子面はたくさんありますが, そのうち単位格子の原点を通らず,原点に最も近い面を選びます.

図では  軸が 1,
軸が 1,  軸が 2,
軸が 2,  軸が 3 となっています.
軸が 3 となっています.
手順 4
これの逆数をとります.いまの場合 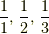 です.
です.
手順 5
ミラー指数は整数を使う約束ですから,
分母の最小公倍数を掛けて同じ比の最小の整数比に直します.
いまの場合 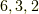 になります.
この面のミラー指数は
になります.
この面のミラー指数は 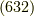 と表記し,「ろく・さん・に・めん」と読みます.
と表記し,「ろく・さん・に・めん」と読みます.

交点がマイナス方向で座標軸を切ったときは指数の上に  を付けて表記します.
を付けて表記します.

上の図のように 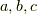 軸を
それぞれ
軸を
それぞれ 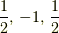 で切る場合は
で切る場合は 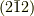 となります.
読み方は「に・いちばー・に・めん」です.
となります.
読み方は「に・いちばー・に・めん」です.
面がある軸と交わらない,つまりある軸と平行なときには,
その軸の指数は0とします(無限遠で交わると考えます).
また,等価な面群は 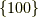 のように中括弧 { } で括ります.
のように中括弧 { } で括ります.
例
つぎの単位格子を例に,格子面とそのミラー指数表示を見てみます.

ちなみにこれは 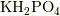 (略称KDP)という結晶の電荷密度です.
VENDというソフトウェアのサンプルをお借りしました.
この図もそのVENDで描きました. 座標軸は
(略称KDP)という結晶の電荷密度です.
VENDというソフトウェアのサンプルをお借りしました.
この図もそのVENDで描きました. 座標軸は

となっています.では,いくつかのミラー指数とその面をご覧ください.

仮に,上の単位格子が立方晶だとすると 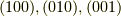 は等価な面です.
立方体は
は等価な面です.
立方体は 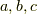 どの軸でも90度回せばもとにもどりますから,
どの軸でも90度回せばもとにもどりますから,
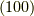 の図を
の図を  軸の回りに90度回せば
軸の回りに90度回せば 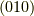 の図になります.
の図になります.
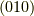 の図を
の図を  軸の回りに90度回せば
軸の回りに90度回せば 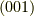 の図になります.
図にはありませんが
の図になります.
図にはありませんが 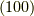 と等価な面はさらに3つあります.
中括弧を使ってこれらをまとめて表すと
と等価な面はさらに3つあります.
中括弧を使ってこれらをまとめて表すと
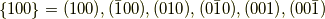
というふうになります.上の例では(立方晶だとして)他にも等価な面群が2セットありますね.