この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
ジョルダン細胞のｎ乗

ジョルダンの標準形で有名なジョルダン細胞のｎ乗を求めます．

ジョルダン細胞

ジョルダン細胞とは，次のｋ次正方行列のことを言います．

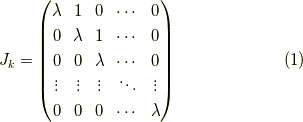
J_k = \begin{pmatrix}\lambda & 1 & 0 & \cdots & 0 \\0 & \lambda & 1 & \cdots & 0 \\0 & 0 & \lambda & \cdots & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \cdots & \lambda\end{pmatrix} \tag{1}

このｎ乗を求めてみましょう．

注目する性質は，対角行列（単位行列の定数倍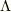） \Lambda

\Lambda = \begin{pmatrix}\lambda & 0 & 0 & \cdots & 0 \\0 & \lambda & 0 & \cdots & 0 \\0 & 0 & \lambda & \cdots & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \cdots & \lambda\end{pmatrix} \tag{2}

のどんな行列とも可換な性質と， べきゼロ行列 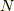N

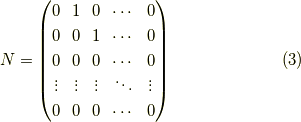
N = \begin{pmatrix}0 & 1 & 0 & \cdots & 0 \\0 & 0 & 1 & \cdots & 0 \\0 & 0 & 0 & \cdots & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \cdots & 0\end{pmatrix} \tag{3}

の持つ，何乗かするとゼロになる性質です． ためしに四次のべきゼロ行列のべき乗を求めてみましょう．

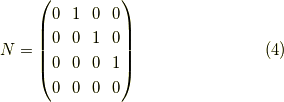
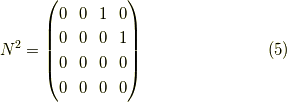
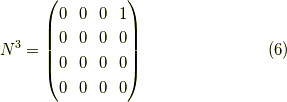
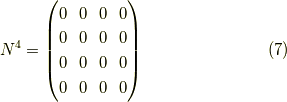
N = \begin{pmatrix}0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\0 & 0 & 0 & 0\end{pmatrix} \tag{4} N^2 = \begin{pmatrix}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0\end{pmatrix} \tag{5} N^3 = \begin{pmatrix}0 & 0 & 0 & 1 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0\end{pmatrix} \tag{6} N^4 = \begin{pmatrix}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0\end{pmatrix} \tag{7}

とこの様に，べき乗すると１のなすラインが上がっていきます．

ここで求めたいのは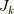， J_k の n 乗，

(J_k)^n = (\Lambda + N)^n \tag{8}

です．二項定理を用います．

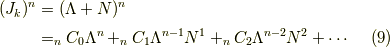
(J_k)^n &= (\Lambda + N)^n \\&= _n C_0 \Lambda^n + _n C_1 \Lambda^{n-1} N^{1} + _n C_2 \Lambda^{n-2} N^{2} + \cdots \tag{9}

ここで 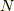N のべき数を昇順にならべました．あるところからは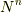， N^n はゼロ行列になります．

簡単な例

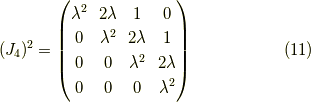
J_4 = \begin{pmatrix}\lambda & 1 & 0 & 0 \\0 & \lambda & 1 & 0 \\0 & 0 & \lambda & 1 \\0 & 0 & 0 & \lambda\end{pmatrix} \tag{10} (J_4)^2 = \begin{pmatrix}\lambda^2 & 2 \lambda & 1 & 0 \\0 & \lambda^2 & 2 \lambda & 1 \\0 & 0 & \lambda^2 & 2 \lambda \\0 & 0 & 0 & \lambda^2\end{pmatrix} \tag{11} (J_4)^3 = \begin{pmatrix}\lambda^3 & 3 \lambda^2 & 3 \lambda & 1 \\0 & \lambda^3 & 3 \lambda^2 & 3 \lambda \\0 & 0 & \lambda^3 & 3 \lambda^2 \\0 & 0 & 0 & \lambda^3\end{pmatrix} \tag{12} (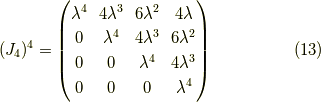J_4)^4 = \begin{pmatrix}\lambda^4 & 4 \lambda^3 & 6 \lambda^2 & 4 \lambda \\0 & \lambda^4 & 4 \lambda^3 & 6 \lambda^2 \\0 & 0 & \lambda^4 & 4 \lambda^3 \\0 & 0 & 0 & \lambda^4\end{pmatrix} \tag{13}

とこの様に簡単にべき乗が求まります．

行列の指数関数

行列の指数関数がジョルダン細胞の場合にも，求まったので書いておきます．

\exp (t J_k) &\equiv \sum_{n=0}^\infty \dfrac{(t J_k)^n}{n!} \\&= \sum_{n=0}^\infty \dfrac{1}{n!} \sum_{i=0}^n \dfrac{n!}{(n-i)!i!} t^n \Lambda^{n-i} N^i \\&= \sum_{i=0}^\infty N^i \dfrac{t^i}{i!} \sum_{n=i}^\infty \dfrac{t^{n-i} \Lambda^{n-i} }{(n-i)!} \\&= \sum_{i=0}^\infty N^i \dfrac{t^i}{i!} \exp (t \lambda) \\&= \sum_{i=0}^{k-1} N^i \dfrac{t^i}{i!} \exp (t \lambda) \tag{14}

よって，例えば，四次なら，

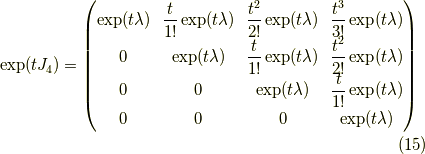
\exp (t J_4)=\begin{pmatrix}\exp (t \lambda) & \dfrac{t}{1!} \exp(t \lambda) & \dfrac{t^2}{2!} \exp(t \lambda) & \dfrac{t^3}{3!} \exp(t \lambda) \\0 & \exp(t \lambda) & \dfrac{t}{1!} \exp(t \lambda) & \dfrac{t^2}{2!} \exp(t \lambda) \\0 & 0 & \exp(t \lambda) & \dfrac{t}{1!} \exp(t \lambda) \\0 & 0 & 0 & \exp(t \lambda)\end{pmatrix} \tag{15}

となります．以上でこの話は終わりです． 続々ベクトルの回転 と比べると面白いかもしれません． ここまで読んだなら，その応用をぜひ知ってください． ジョルダン標準形の指数関数の応用 をご覧あれ． 今日はここまで，お疲れ様でした．