この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
相関関数と畳み込み積分のフーリエ変換
今回は物理とは距離を置いて,物理を勉強する上で僕がつきあたった 数学的問題の一つを,厳密さに欠けますが,書こうと思います. 厳密には,積分の順序を交換する時,それぞれの積分が絶対収束することを 言わねばなりません.
相関関数
実数の物理量 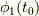 と,
と, 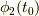 の相互相関関数
の相互相関関数 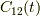 とは,
とは,
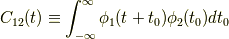
と定義されます.注意しておくこととして,相互相関関数は,自己相関関数( 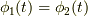 の時)と違い,偶関数にはなりません.
の時)と違い,偶関数にはなりません.
相関関数のフーリエ変換
これをフーリエ変換するとどうなるか,と言うのが,今回の問題です. やってみますと,
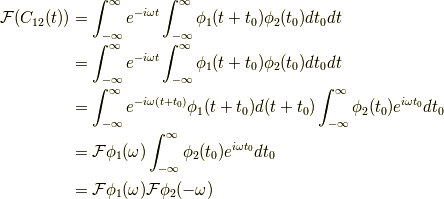
となります.ここで, 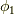 と
と 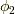 を入れ替えれば,
を入れ替えれば, 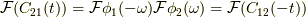 が成立します.
が成立します.
余談ですが,もしかすると,ヤコビアンに関する知識が必要かもしれません.
つまりは, 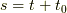 と置くと,
と置くと, 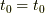 ,
, 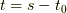 より,
より,
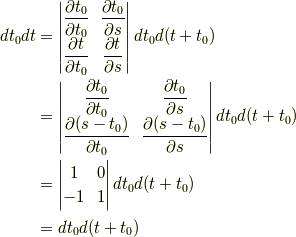
です.
畳み込み積分とフーリエ変換
畳み込み積分というものを定義します.
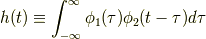
これもフーリエ変換してみましょう.
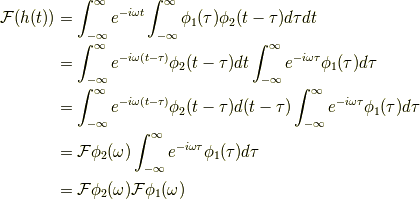
こうなりました.何かの参考になれば幸いです.
それでは,今日はこの辺で.