この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
準同型写像
ここまでに,群の性質や,群の働き方,部分群にまつわる様々なトピックを勉強してきました.いわば,いままでは群そのものについて勉強してきたとも言えるでしょう.
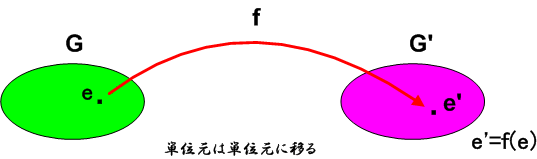
この記事では少し趣向を変えて,二つの群,  と
と  があったときに,群
があったときに,群  の元から群
の元から群  の元へ対応関係がつけられるかを考えます.今までは二つの群が同型である,という意味を,やや曖昧にしたまま直観的に使ってきましたが,二つの群の対応関係をきちんと考えることで,群の同型という意味がはっきりしてきます.
の元へ対応関係がつけられるかを考えます.今までは二つの群が同型である,という意味を,やや曖昧にしたまま直観的に使ってきましたが,二つの群の対応関係をきちんと考えることで,群の同型という意味がはっきりしてきます.
実は,対象そのものを一つだけ考えるよりも,対象を写像してみることで,結局は対象の構造がよく分かる,ということが数学ではよくあります.写像の話題が大事なのは,一つには,写像を考えることで代数構造への理解が深まるという理由が考えられます.
準同型
何か関数  があり,群
があり,群  の元と,群
の元と,群  の元とが関数によって対応づけられるとします.ある集合の元を,異なる集合の元に対応づける関数関係を 写像 と呼ぶのでした.集合論や線形代数を既に勉強したことがある人ならば,聞いたことがあると思います.
の元とが関数によって対応づけられるとします.ある集合の元を,異なる集合の元に対応づける関数関係を 写像 と呼ぶのでした.集合論や線形代数を既に勉強したことがある人ならば,聞いたことがあると思います.
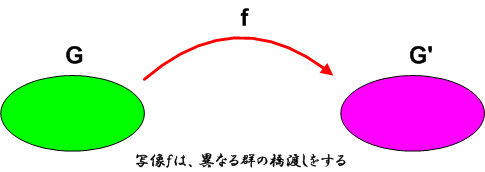
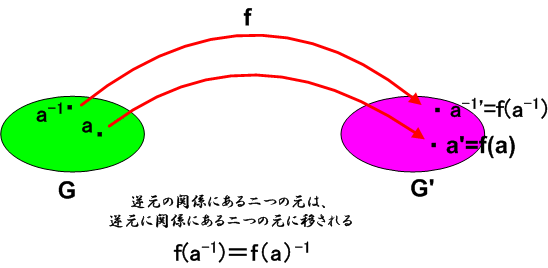
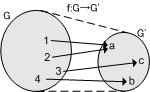
つまり,写像  によって,群
によって,群  の元は,何らかの方法により群
の元は,何らかの方法により群  の元に移されます.しかし
の元に移されます.しかし  の働き方にだって色々あるはずです.例えば
の働き方にだって色々あるはずです.例えば  の一つの元に対して
の一つの元に対して  の複数の元が滅茶苦茶に対応する [*] とか,全ての
の複数の元が滅茶苦茶に対応する [*] とか,全ての  の元が
の元が  の単位元に移されてしまうとか,そんな写像の方法だって考えられます(だから,上の絵では元の対応関係を,わざといい加減にしておきました).
の単位元に移されてしまうとか,そんな写像の方法だって考えられます(だから,上の絵では元の対応関係を,わざといい加減にしておきました).
| [*] | 厳密には多価の対応関係は写像ではない.とのご指摘を頂きました.ここでは,対応関係がでたらめなことを意図したものだとお考えください. |
しかし,実際に使う場面では,そのような変チクリンな写像は,あまり便利ではありません.群論で一番大事なのは,次のように定義される, 準同型写像 と呼ばれる写像です.
definition
写像  が群
が群  の元
の元 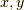 に作用するとき,
に作用するとき, 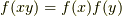 を満たすものを準同型写像という.
を満たすものを準同型写像という.
なぜ,準同型写像が群論ではそんなに重要なのかを次に考えていきましょう.写像先の群  の元には,以後全てダッシをつけて
の元には,以後全てダッシをつけて 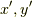 のように表記することにします.
のように表記することにします.
演算が移されること
群  の元
の元  の積が,準同型写像
の積が,準同型写像  によってどう移されるかを見ます.群
によってどう移されるかを見ます.群  の元について
の元について 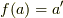 ,
, 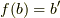 と定義すると,準同型写像の定義式より次式が言えるでしょう.
と定義すると,準同型写像の定義式より次式が言えるでしょう.
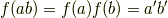
すなわち,準同型写像によって群  の元
の元 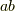 が,群
が,群  の元
の元 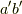 に移されるということです.群
に移されるということです.群  の元の間に,どのような演算が成り立つか,ということは(積の形に表現はしてありますが)具体的には,明らかではないことに注意してください.とにかく,群
の元の間に,どのような演算が成り立つか,ということは(積の形に表現はしてありますが)具体的には,明らかではないことに注意してください.とにかく,群  で閉じている「ある演算」が,群
で閉じている「ある演算」が,群  で閉じている「ある演算」(同じ演算ではないことに注意してください)に移されたということです.
で閉じている「ある演算」(同じ演算ではないことに注意してください)に移されたということです.
| [†] | 演算は同じものではありませんが,演算が演算に移った,ということは,群の構造が準同型写像によってある程度移されるということです.これは嬉しいことです.ただし,具体的に個々の準同型写像が一体どのようなものかが不明なのですから,  の構造について,これだけの情報では,より具体的なことは言えません.しかし,群 の構造について,これだけの情報では,より具体的なことは言えません.しかし,群  は群 は群  を写像することで得られる群ですから,大抵の場合,群 を写像することで得られる群ですから,大抵の場合,群  の構造を「ある程度は」反映した構造になっているものです. の構造を「ある程度は」反映した構造になっているものです. |
単位元
まず,群  の単位元
の単位元  は,準同型写像
は,準同型写像  によって次のように移されます.
によって次のように移されます.
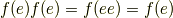
左辺と中辺は準同型写像の定義そのまま,中辺と右辺の変形には 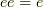 という関係を使っただけです.
という関係を使っただけです. 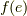 は群
は群  の元のはずですから,逆元
の元のはずですから,逆元 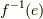 が存在するはずです.
が存在するはずです. 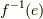 を両辺から掛けると,次式を得ます.
を両辺から掛けると,次式を得ます.
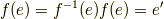
つまり,準同型写像によって 単位元は単位元に移されます . これは,非常に便利な性質です.
逆元
同様に,  のある元
のある元  の逆元
の逆元 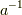 がどのように写像されるかを見てみましょう.
がどのように写像されるかを見てみましょう.
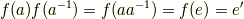
つまり,群  において,
において, 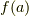 と
と 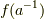 は逆元の関係になっているということです.準同型写像によって 逆元は逆元に移される ということが分かりました.これを,次のように書いておきましょう.
は逆元の関係になっているということです.準同型写像によって 逆元は逆元に移される ということが分かりました.これを,次のように書いておきましょう.
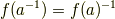
| [‡] | 準同型写像によって,単位元や逆元はそれぞれ単位元や逆元にうつされ,また,移された先の群でも,元同士の演算は閉じていることが分かりました.つまり,準同型写像は『群の構造を保存する写像』だと言うことができます.だから準同型写像が群論で重要なわけです.しかし  が群になるからといって,ただちに が群になるからといって,ただちに  と と  が同型だとは言えません.同型の定義には,後に見ますが,もっと強い条件が必要です.『群の構造を保存する』という言い回しと,『群が同型である』というのは全然別のことですから,慣れるまで言葉の意味に注意して下さい.準同型写像の"準"は,その辺りの事情を反映した,なかなか絶妙な命名です. が同型だとは言えません.同型の定義には,後に見ますが,もっと強い条件が必要です.『群の構造を保存する』という言い回しと,『群が同型である』というのは全然別のことですから,慣れるまで言葉の意味に注意して下さい.準同型写像の"準"は,その辺りの事情を反映した,なかなか絶妙な命名です. |
| [§] | 数学では『構造を保存する写像』を特に"射"と呼ぶのでした.準同型写像は,上に見たように群の構造を保存しますから,群論における射である,と言えるでしょう.いま私達が考えているのとは違う数学的構造,例えば位相構造における射は,二つの集合の連続性を保つような写像を射と考えます.数学には,いま私達が勉強している代数構造の他に,位相構造,順序構造などの構造があるのでした( 群について基本的なこと 参照).いま,私達は『群構造を保つ射として準同型写像を考えているんだ』という立場を諒解しておいて下さい.というのは,私達はいま群論を勉強しているからです. |
準同型写像の合成
最後に,群  から群
から群  への準同型写像を
への準同型写像を  , 群
, 群  から群
から群  への準同型写像を
への準同型写像を  として,これらの合成写像
として,これらの合成写像 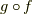 がどのように移されるかを見ます.
がどのように移されるかを見ます. 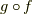 を
を 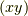 に作用させ,あとは準同型写像の定義式に当てはめていくだけです.
に作用させ,あとは準同型写像の定義式に当てはめていくだけです.
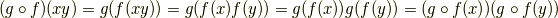
準同型写像の合成は,やはり準同型写像になることが分かりました.
単準同型,全準同型,同型
次に,準同型写像によって,群  が群
が群  にどのように移されるかによって,準同型写像を,少し種類分けしたいと思います.(先ほどは,単位元や逆元など,特定の元にだけ着目して準同型写像の働き方を見ましたが,一般的には,まだ写像の仕方を決めていません.)
にどのように移されるかによって,準同型写像を,少し種類分けしたいと思います.(先ほどは,単位元や逆元など,特定の元にだけ着目して準同型写像の働き方を見ましたが,一般的には,まだ写像の仕方を決めていません.)
難しい写像は出てきませんが,ここで十分に写像の基礎を復習をしている訳にはいきません.『どうも難しい...(・_・)』と感じる人は,自分で集合論や線形代数を復習してみてください.
単射
群  の元から,群
の元から,群  の元への写像により,
の元への写像により,  の元が必ず
の元が必ず  の一つの元に写像されるとき,このような写像を 単射 と呼びます.
の一つの元に写像されるとき,このような写像を 単射 と呼びます.  の中で異なる二つの元は,必ず
の中で異なる二つの元は,必ず  の中でも異なる二つの元に移されるという, 一対一の関係 が単射のポイントです.当然,
の中でも異なる二つの元に移されるという, 一対一の関係 が単射のポイントです.当然,  が
が  よりも小さな群ということはあり得ませんが(少なくとも同じ位数でなければならないはずです),
よりも小さな群ということはあり得ませんが(少なくとも同じ位数でなければならないはずです),  の方が大きな群であれば,
の方が大きな群であれば,  の元の中には
の元の中には  に対応する元を持たないものも含まれるでしょう.
に対応する元を持たないものも含まれるでしょう.

つまり,単射の場合,一般に  の
の  による像は,
による像は,  の部分群になると言えます.単射の写像により二つの群が準同型の場合,これを 単準同型 と呼びます.(間違えて単純同型と書かないように注意しましょう.)
の部分群になると言えます.単射の写像により二つの群が準同型の場合,これを 単準同型 と呼びます.(間違えて単純同型と書かないように注意しましょう.)
例えば,正の整数で,ある整数  に対し,それよりも
に対し,それよりも 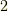 大きい数
大きい数 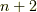 を考え(例えば
を考え(例えば 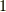 と
と 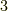 ,
, 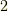 と
と 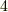 という具合),これを
という具合),これを 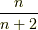 という分数に対応させます.これによって正の整数は有理数に対応づけられますし,有理数の方からも
という分数に対応させます.これによって正の整数は有理数に対応づけられますし,有理数の方からも 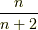 の形で表わされる有理数が一つに決まります.よって,この写像は一対一で,単射だと言えます.しかし,有理数の中には
の形で表わされる有理数が一つに決まります.よって,この写像は一対一で,単射だと言えます.しかし,有理数の中には 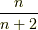 の形で表わせないものもたくさんありますから,有理数の方が大きな集合で,この写像による対応関係はちょうど上図のようになります.確認してみて下さい.
の形で表わせないものもたくさんありますから,有理数の方が大きな集合で,この写像による対応関係はちょうど上図のようになります.確認してみて下さい.
全射
群  の全ての元を写像させたものが
の全ての元を写像させたものが  になるとき,この写像を 全射 と呼びます.写像によって,
になるとき,この写像を 全射 と呼びます.写像によって,  の一つの元は
の一つの元は  の一つの元へ移されますので,一つの
の一つの元へ移されますので,一つの  の元に対して複数の
の元に対して複数の  の元が対応することはありません.しかし逆に,複数の
の元が対応することはありません.しかし逆に,複数の  の元が,同一の
の元が,同一の  の元に写像される可能性はあります.一般的には,全射の対応関係は,次図のように表せるでしょう.全射の写像により二つの群が準同型である場合,これを 全準同型 と呼びます.
の元に写像される可能性はあります.一般的には,全射の対応関係は,次図のように表せるでしょう.全射の写像により二つの群が準同型である場合,これを 全準同型 と呼びます.
例えば,実数 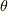 に複素数
に複素数 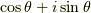 を対応させることで,実数の乗法群
を対応させることで,実数の乗法群  を複素数の乗法群
を複素数の乗法群  に対応させることができます.これを
に対応させることができます.これを 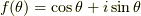 と表わしましょう.
と表わしましょう.  がなりたつので,この写像は準同型写像になっています.しかし,例えば
がなりたつので,この写像は準同型写像になっています.しかし,例えば  と
と 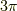 がどちらも
がどちらも 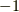 に移されるように,
に移されるように, 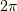 ずれた実数は,どれも同じ複素数に移されてしまいますので,この写像は全射なのです.
ずれた実数は,どれも同じ複素数に移されてしまいますので,この写像は全射なのです.
同型
全射と単射は異なる概念ですから,この二つを組み合わせると,計四つのパターンが考えられます.頭を整理するために,それぞれがどのような場合を意味しているのかを納得するまで考えてみてください.

特に『単射でもあり全射でもある』写像を 同型写像 と呼びます.上図の4番目のものです.
| [¶] | 同型写像では,二つの元の間に,過不足なく一対一の対応関係が成り立ちますので,  から から  の写像も, の写像も,  から から  の写像も行ったり来たり自由自在です.つまり,同型写像には逆写像があるということです.逆写像の存在こそが,同型写像の最大の特徴であり,便利な点です.一般の準同型写像では,一意的な逆写像は無いかも知れないという点をもう一度確認してみてください. の写像も行ったり来たり自由自在です.つまり,同型写像には逆写像があるということです.逆写像の存在こそが,同型写像の最大の特徴であり,便利な点です.一般の準同型写像では,一意的な逆写像は無いかも知れないという点をもう一度確認してみてください. |
| [#] | 同型写像の定義として『 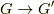 が準同型写像であり, が準同型写像であり, 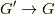 も準同型写像であるとき,この写像を同型写像と呼ぶ』としても良いでしょう. も準同型写像であるとき,この写像を同型写像と呼ぶ』としても良いでしょう. |
| [♠] | 準同型写像の定義式は,いま積の形で書かれていますが,もしも集合になりたつ演算が可換ならば,もちろん和の形で書いても良いのです.すると,準同型写像の定義式は 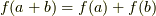 になりますね.線形代数を勉強した人なら,この形は線形写像という名前で見覚えがあると思います. 線形写像は可換な準同型写像の一種だった のです.(ただし線形写像には,もう一つスカラー倍演算という性質が必要です.)この記事では,集合として群を考えていますが,集合としてベクトル空間を考えるのが線形代数です. になりますね.線形代数を勉強した人なら,この形は線形写像という名前で見覚えがあると思います. 線形写像は可換な準同型写像の一種だった のです.(ただし線形写像には,もう一つスカラー倍演算という性質が必要です.)この記事では,集合として群を考えていますが,集合としてベクトル空間を考えるのが線形代数です. |
自己準同型,自己同型
群  を
を  自身へ移す準同型写像を 自己準同型 と呼び,群
自身へ移す準同型写像を 自己準同型 と呼び,群  を
を  自身へ移す同型写像を 自己同型 と呼びます.群
自身へ移す同型写像を 自己同型 と呼びます.群  の自己同型を
の自己同型を  のように書きます.
のように書きます.
自己同型は写像ですが,自己同型  を何度合成しても,やはり
を何度合成しても,やはり  の元は
の元は  に移されますから,いわば写像の合成に関して閉じている,と言えます.同型写像なので逆写像もあります.よって,逆写像を逆元,恒等写像を単位元として,自己同型写像の全体は,やはり群の構造を持ちます.これを 自己同型群 と言います.写像を元とする群なんていうのもあるんですね.
に移されますから,いわば写像の合成に関して閉じている,と言えます.同型写像なので逆写像もあります.よって,逆写像を逆元,恒等写像を単位元として,自己同型写像の全体は,やはり群の構造を持ちます.これを 自己同型群 と言います.写像を元とする群なんていうのもあるんですね.
| [♥] | 自己同型群は,ガロア理論で非常に重要な役割を果たします.何となく覚えておいて下さい. |
準同型写像の核
さて,話が同型写像にまで行ってしまいましたが,また準同型写像に戻ります.写像には単射や全射といった種類があったことを確認してください.
群  の単位元
の単位元  は必ず群
は必ず群  の単位元
の単位元 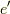 に移されるということでしたが,もし写像が全射ならば,
に移されるということでしたが,もし写像が全射ならば,  の中には他にも
の中には他にも 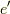 に移される元があるかも知れない,と考えられます(よく分からない人は,もう一度,全射の節を復習して下さい).
に移される元があるかも知れない,と考えられます(よく分からない人は,もう一度,全射の節を復習して下さい).
群  の部分集合で,準同写像によって
の部分集合で,準同写像によって 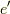 に移されてしまうものを Gの核 と呼びます.ドイツ語で核を
に移されてしまうものを Gの核 と呼びます.ドイツ語で核を 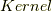 と言いますが,日本語でも核と言わずに カーネル とそのまま呼ぶ人もいます.
と言いますが,日本語でも核と言わずに カーネル とそのまま呼ぶ人もいます.
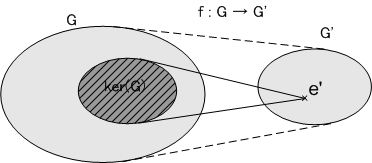
核の大きさは,もちろん準同型写像によって変わります.最低で元1つ(単位元のみ),最大で群  そのものです.準同型写像の核について,次の定理がとても重要です.
そのものです.準同型写像の核について,次の定理がとても重要です.
theorem
準同型写像  の核
の核 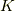 は正規部分群になります
は正規部分群になります
proof
群  の核
の核 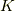 に属する二つの元
に属する二つの元  に対し,準同型写像の定義より,
に対し,準同型写像の定義より, 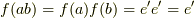 がなりたちます.よって,
がなりたちます.よって,  の積
の積 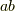 も核
も核 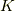 の元であるはずで,
の元であるはずで, 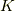 は演算について閉じていることが分かります.また,準同型写像によって逆元は逆元に移されるということでしたが,
は演算について閉じていることが分かります.また,準同型写像によって逆元は逆元に移されるということでしたが, 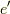 の逆元は
の逆元は 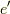 自身ですから,
自身ですから,  や
や  の逆元
の逆元 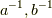 も核
も核 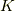 に入っていなければならないことが分かります.
に入っていなければならないことが分かります.  の単位元
の単位元  が
が 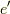 に移されることは既に見ました.これらの結果より,核
に移されることは既に見ました.これらの結果より,核 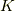 は部分群になっていることが分かります.最後に,核
は部分群になっていることが分かります.最後に,核 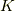 が正規部分群であることを示します.準同型写像の定義より,
が正規部分群であることを示します.準同型写像の定義より, 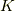 の任意の元
の任意の元 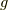 に対し
に対し 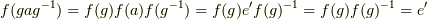 が言え,
が言え,  も
も 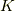 の元であることが示せました.■
の元であることが示せました.■
| [♦] | 正規部分群の概念は群論の中でも非常に重要です.順番としては剰余類や商群から出てきた概念ですが,より現代的な捉え方としては,正規部分群を準同型写像の核として定義した方がスマートかも知れません. |