この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ハミルトニアンとラグランジアンの全微分形
この記事では,ハミルトニアンとラグランジアンの全微分形を確認します. その後で,特に一粒子の調和振動子に対する表式を確認します.
ハミルトニアンの全微分形
時間に依存しないハミルトニアンに対して, 正準方程式は,時間微分をドットで表すと,


ですね.よって,ハミルトニアンの全微分は,
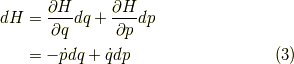
となります.
ラグランジアンの全微分形
式  にルジャンドル変換を行います.
にルジャンドル変換を行います.

ですから,
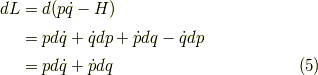
となります.
調和振動子の場合
調和振動子の運動方程式は,

です.この関係を用いて,まずは 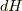 を
を 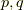 で表します.
で表します. 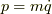 より,
より,
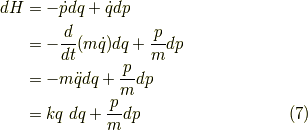
とこの様になります.そして,ラグランジアンの方は, 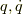 で表しますから,
で表しますから,
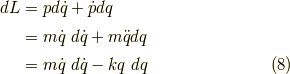
となります.そして,これらの量は状態量であるので,
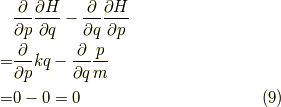
や,
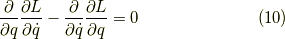
が成立し,適当な積分路で積分してやれば,積分路の端点 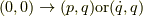 が同じである限り,
どんな積分路であろうとも,
が同じである限り,
どんな積分路であろうとも,


となります.それでは今日はこの辺で.