この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
弱い力の変換則(非可換ゲージ場SU(2))
この記事では弱い力の変換性

の右辺第二項の計算を見ます.右辺第一項は大域的変換で"3次元アイソスピン空間"での回転を表します.第二項は局所的な変換対称性を表し, 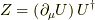 と置きます.参考文献として,コッティンガム,グリーンウッド共著,樺沢宇紀訳『素粒子標準模型入門』(丸善出版)から,基本設定を使わせて頂きます.
と置きます.参考文献として,コッティンガム,グリーンウッド共著,樺沢宇紀訳『素粒子標準模型入門』(丸善出版)から,基本設定を使わせて頂きます.
基本設定
まず,群  の任意の要素は3つの実数
の任意の要素は3つの実数 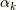 とパウリ行列
とパウリ行列  を用いて,
を用いて,

と書けます.そして,パウリ行列は

です.弱い力の非可換ゲージ場
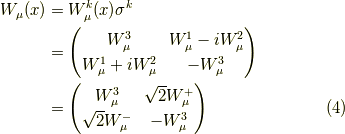
を表します.
量子場としての 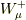 は
は 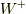 ボゾンの消滅演算子(
ボゾンの消滅演算子(  ボゾンの生成演算子)であり,
また,
ボゾンの生成演算子)であり,
また, 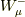 は
は  ボゾンの消滅演算子(
ボゾンの消滅演算子( 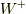 ボゾンの生成演算子)です.
そして,
ボゾンの生成演算子)です.
そして, 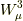 は
は  ボゾンと光子
ボゾンと光子  の混合粒子からなる中性粒子の生成消滅演算子(Zボゾンの反粒子はZボゾンであり,光子γの反粒子も光子γです.すみません.本当に反粒子が自己自身の場合,生成演算子と消滅演算子が同じものなのか,分かりませんでした.光子には小出昭一郎『量子力学II』裳華房とかだと,生成演算子と消滅演算子は違うものみたいなんですが..)
また,下添え字
の混合粒子からなる中性粒子の生成消滅演算子(Zボゾンの反粒子はZボゾンであり,光子γの反粒子も光子γです.すみません.本当に反粒子が自己自身の場合,生成演算子と消滅演算子が同じものなのか,分かりませんでした.光子には小出昭一郎『量子力学II』裳華房とかだと,生成演算子と消滅演算子は違うものみたいなんですが..)
また,下添え字 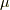 はベクトルポテンシャル
はベクトルポテンシャル 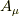 と同じく座標変数
と同じく座標変数 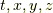 でラベルされます.
でラベルされます.
SU(2)の元
さて, 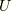 の具体形を見てみましょう.リー群
の具体形を見てみましょう.リー群  の元と言うことで表現はいくつかあるようですが,
取りあえず今回はパウリ行列を選びました.
式
の元と言うことで表現はいくつかあるようですが,
取りあえず今回はパウリ行列を選びました.
式 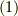 は,
は,
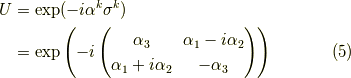
ここで,
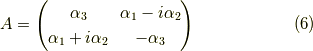
と置くと, 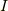 を単位行列,
を単位行列, 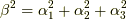 として,
として,

が成立します.つまり,これで  の計算が実行でき,
の計算が実行でき,

となります.これは確かに
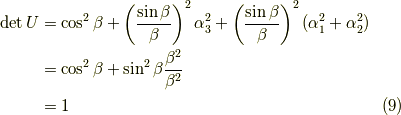
より,ユニタリー行列です.
Zの計算
式 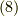 を微分して,
を微分して,  を掛ければ目的の
を掛ければ目的の 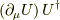 が得られる訳です.
ここで,
が得られる訳です.
ここで, 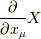 を
を 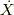 で表すことにします.
で表すことにします.  を
を 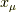 で微分するので,各
で微分するので,各 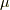 に関して,構造は同じと分かりますから,そう略記できる訳です.
に関して,構造は同じと分かりますから,そう略記できる訳です.
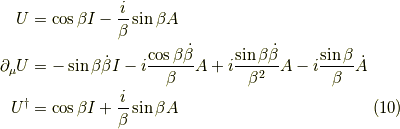
より,
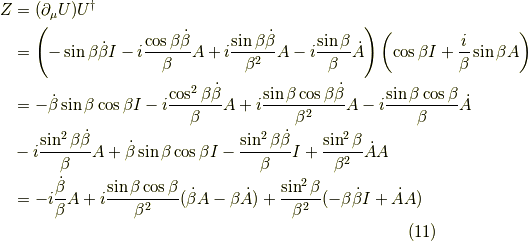
ここで,
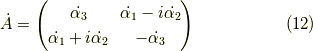
であり,
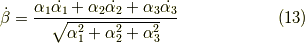
であり,
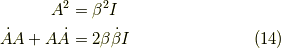
より,更に計算を進めて,
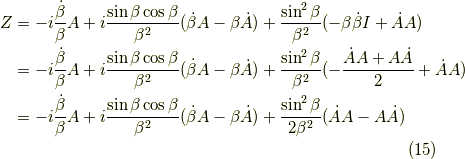
となります. ただし,

として,
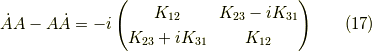
となっています. 力技でここまで来ましたが,もっと エレガントな方法 をご紹介頂いたので,リンクを張っておきます. 今日はこの辺で,お疲れさまでした.