この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
擬テンソル
ベクトルとは,直交変換に際して次のような変換則に従う量と定義されました.

これとそっくりな, 擬ベクトル という量が 反対称テンソルと軸性ベクトル に出てきました.

違いは, 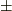 という記号があるかないかですが,擬ベクトルは,右手系と左手系が入れ替わるような座標変換に対しては,その符号を入れ替わるのでした.(擬ベクトルを,軸性ベクトルとも呼びます.)擬テンソルのこの性質を高階のテンソルにまで一般化し,やはり右手系・左手系の交換に伴って符号を変えるような量を, 擬テンソル と呼びます.擬テンソルの一般的な定義は,この座標変換を表わす行列の行列式
という記号があるかないかですが,擬ベクトルは,右手系と左手系が入れ替わるような座標変換に対しては,その符号を入れ替わるのでした.(擬ベクトルを,軸性ベクトルとも呼びます.)擬テンソルのこの性質を高階のテンソルにまで一般化し,やはり右手系・左手系の交換に伴って符号を変えるような量を, 擬テンソル と呼びます.擬テンソルの一般的な定義は,この座標変換を表わす行列の行列式 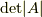 を用いて,次のように定式化します.
を用いて,次のように定式化します.
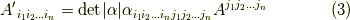
この 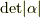 が,
が, 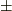 になることを次のセクションで確認します.
になることを次のセクションで確認します.
座標変換の行列式
まずはベクトルの変換から考えます.直交座標系で考え,座標変換前の基底ベクトル 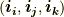 ,変換後の基底ベクトルを
,変換後の基底ベクトルを 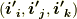 とします.直交座標系で考えているので,基底については次の関係式がなりたちます.
とします.直交座標系で考えているので,基底については次の関係式がなりたちます.
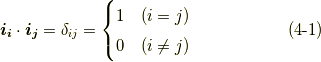
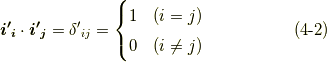
また,新旧の座標系の間には,次図のような関係があります.図中 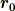 は旧座標系の原点,
は旧座標系の原点, 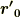 は新座標系の原点とします.
は新座標系の原点とします.
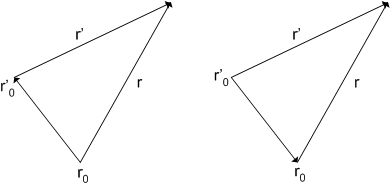
このとき次の関係式が分かるでしょう.


これより, 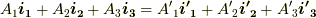 として,成分に関して次式がなりたちます.ダッシュのつく位置に気をつけてください.両辺とも,縮約により
として,成分に関して次式がなりたちます.ダッシュのつく位置に気をつけてください.両辺とも,縮約により 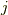 について和を取る形になっています.
について和を取る形になっています.
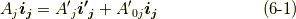
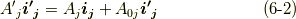
式  の両辺に
の両辺に 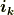 を,式
を,式  の両辺に
の両辺に 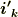 を作用させて内積を取ると,基底の直交関係より,次式を得ます.
を作用させて内積を取ると,基底の直交関係より,次式を得ます.
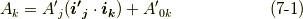
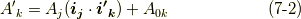
次に,式 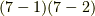 中の内積部分を,上手くテンソルの形に直すことを考えます.基底の変換則
中の内積部分を,上手くテンソルの形に直すことを考えます.基底の変換則 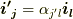 の両辺と
の両辺と 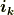 の内積を取ることで,式
の内積を取ることで,式  中の内積部分
中の内積部分 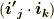 を次のように表わせるでしょう.
を次のように表わせるでしょう.
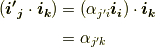
同様に, 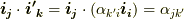 となります.一方,
となります.一方, 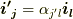 の両辺と
の両辺と 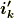 の内積を取ると次式を得ます.
の内積を取ると次式を得ます.
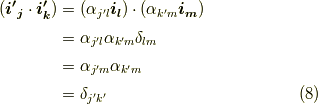
導出が長くなりましたが,式 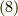 が求めていた式です.テンソルの関係式
が求めていた式です.テンソルの関係式 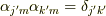 を行列の形に書き換え,両辺の行列式を取ります.
を行列の形に書き換え,両辺の行列式を取ります.
![{\rm det} [\alpha _{j'm} \alpha _{k'm} ]= {\rm det} [\delta_{j'k'}]=1](http://hooktail.maxwell.jp/kagi/ab50cb1b8daba3919547ec2009df552c.png)
クロネッカーのデルタの行列式は添字に関わらず 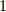 です.また,
です.また, ![[\alpha _{j'm}]](http://hooktail.maxwell.jp/kagi/0c7255b244d3b16753cc202c643b9921.png) と
と ![[ \alpha _{k'm} ]](http://hooktail.maxwell.jp/kagi/0f025b14b425e45a8bf5ff485be635b7.png) の行列式は同じはずですから,左辺は
の行列式は同じはずですから,左辺は ![({\rm det} [\alpha _{j'm} ])^{2}](http://hooktail.maxwell.jp/kagi/0e365d835ca2e145fa7ee9accfa9ea8c.png) だと考えても良く,結局次式を得ます.
だと考えても良く,結局次式を得ます.
![{\rm det} [\alpha _{j'm} ]= \pm 1](http://hooktail.maxwell.jp/kagi/0cb2cbe31b9140521747da9027e9cc15.png)
式 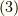 は次のように書けます.
は次のように書けます.
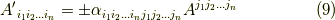
式 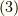 もしくは式
もしくは式 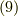 を擬テンソルの定義式とします.符号は,右手系と左手系が入れ替わる座標変換においては
を擬テンソルの定義式とします.符号は,右手系と左手系が入れ替わる座標変換においては 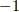 ,右手系と左手系が入れかわらない座標変換においては
,右手系と左手系が入れかわらない座標変換においては 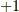 に取ります.
に取ります.