この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
リー微分のイメージ(ベクトルによるベクトルのリー微分)

この記事では，ベクトルによるベクトルのリー微分を説明します．

\mathcal{L}_X Y = [X,Y] \tag{1}

と書かれても，よく分からず途方に暮れた人は多いのではないでしょうか？ リー微分は分かってしまえば簡単です．

二つの流れを用意する

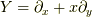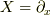二次元平面上の二つの流れを用意します． まず， 微分幾何学における流れの具体例 で取り扱った放物線状のベクトル場 Y = \partial_x + x \partial_y と， X = \partial_x と言う， x 軸の正の方向に単位量だけ流れている流れを用意します．

ここで，

\mathcal{L}_X Y &= [X,Y] \\&= \dfrac{\partial}{\partial x} \left( \dfrac{\partial}{\partial x} + x \dfrac{\partial}{\partial y} \right)- \left( \dfrac{\partial}{\partial x} + x \dfrac{\partial}{\partial y} \right) \left( \dfrac{\partial}{\partial x} \right) \\&= \left( \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial}{\partial y} + x \dfrac{\partial^2}{\partial x \partial y} \right)-\left( \dfrac{\partial^2}{\partial x^2} + x \dfrac{\partial^2}{\partial x \partial y} \right) \\&= \dfrac{\partial}{\partial y} \tag{2}

となりました．これは，何を表しているかと言うと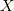， X の流れに単位量だけ乗った後 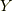Y の流れに単位量だけ乗った結果から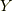， Y の流れに単位量だけ乗った後 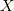X の流れに単位量だけ乗った結果を引いたベクトルを表しています．

図を見れば明らかでしょう．

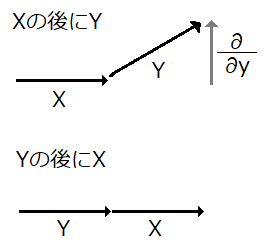
chromel-whatMeansLieDerivative-01.png

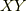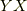これは，参考文献にもある通りです． XY も YX も二階の微分を含むのでベクトルではないのですが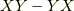， XY-YX はうまく相殺して一階の微分となっていることに注意して下さい．実はこの記事はリー微分の全てではなくて，多様体上のリー微分になると，基底である 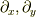\partial_x,\partial_y 等の変換も扱わねばならないようです．僕が理解した時には追って報告しようと思います．今日はここまで，お疲れさまでした．