この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
畳み込み積分の微分
この記事では,
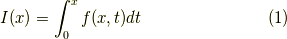
の微分,
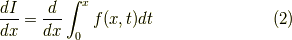
を求めた後,畳み込み積分の微分,
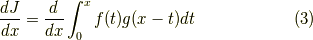
を求めます.
証明1:微分の定義に従う
まずは微分の定義に従ってこの 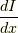 を求めてみましょう.
を求めてみましょう.
まずは復習です. 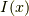 の微分の定義は,
の微分の定義は, 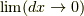 の時,
の時,
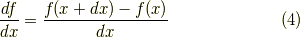
でしたね.よって, 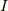 の微分は,
の微分は, 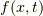 の
の 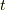 に関する原始関数を
に関する原始関数を 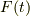 とおくと(つまり,
とおくと(つまり, 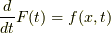 であり,ここで
であり,ここで 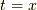 とおけば,
とおけば, 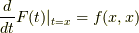 となります.),適宜
となります.),適宜 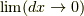 ととれば,
ととれば,
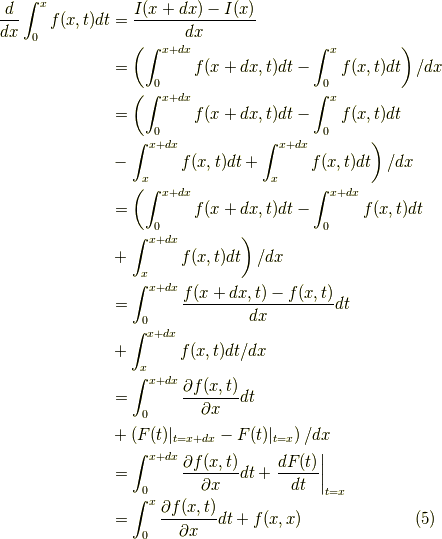
よって結果だけを書くと,
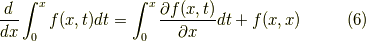
となります.これだけではちょっと不安なので,同じ計算を別の方法でやってみます.
証明2:多変数の微分として見る
まず,  と
と 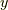 をパラメータ
をパラメータ  の変数としてみます.最後に
の変数としてみます.最後に 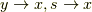 とします.そこで,考えるのは
とします.そこで,考えるのは
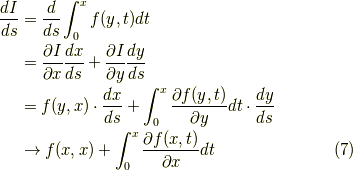
となり,同じ結果になりました.どうやら正しそうですね.一応注意しておくと, 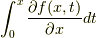 は,
は, 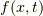 を
を 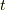 を定数と見て
を定数と見て  で偏微分したのち,今度は
で偏微分したのち,今度は  を定数と見て
を定数と見て 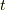 で積分したものです.
で積分したものです.
証明3:合成関数の微分として見る
基本的には証明2と同じですが,よりシンプルだということで記しておきます.
積分の二つのxを別の変数と見て,二変数の関数  と
と 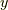 との関数と見なします.どちらを
との関数と見なします.どちらを 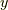 としても最後に
としても最後に 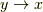 とするので,同じことになります.すると,求めたい微分は
とするので,同じことになります.すると,求めたい微分は
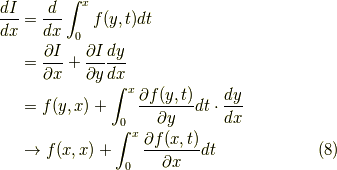
と同じ結果となります.
具体例で確かめる
では,得られた結果を具体例で確認してみましょう. 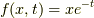 を計算してみます.
を計算してみます.
![\dfrac{d}{dx} \int_0^x f(x,t)dt &= \dfrac{d}{dx} \int_0^x x e^{-t} dt \\&= \dfrac{d}{dx} \left[ -x e^{-t} \right]_{t=0}^{t=x} \\&= \dfrac{d}{dx} \left( -x e^{-x} + x \right) \\&= (x-1) e^{-x} + 1 \tag{9}](http://hooktail.maxwell.jp/kagi/aa9f6f65aa31ea0bf62a213702b35107.png)
となります.ここで, 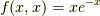 であり,
であり, 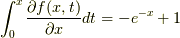 ですから,両者は一致します.
ですから,両者は一致します.
畳み込み積分の微分
関数 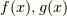 の畳み込みとは以下のような積分になります.
の畳み込みとは以下のような積分になります.
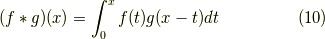
これは, 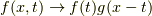 として,先ほど得られた結果を用いれば良く,
として,先ほど得られた結果を用いれば良く,
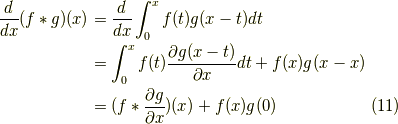
と分かります.それでは,今日はこの辺で.お疲れ様でした.