この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。リンクを正しく張れていないところが存在しますのでご注意ください。正式公開まで、いましばらくお待ちください。
divは完全情報か？

どうも，クロメルです．面白い話を見つけました．お付き合いくださるとうれしいです．普通，ベクトルで内積をとると情報が失われます．つまり，内積だけを与えられて元のベクトルを復元せよ．と言っても不可能なのです．では，ナブラを使ったダイバージェンス（発散）は，内積みたいだけど，情報は失われるのか？と言うのが今回のテーマです．

基本法則

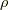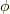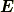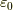静電気学を扱います．基本法則は次の二つです． $\rho$ は電荷密度，: $\phi$ はポテンシャル， $\bm{E}$ は電場， $\varepsilon_0$ は真空の誘電率です．

$\rm{div}\bm{E}=\dfrac{\rho}{\varepsilon_0} \tag{1} \\\bm{E} = -\rm{grad} \phi \tag{2}$

結論から言うと，ダイバージェンスは情報を失います．次の二つを見て下さい．同じ 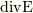$\rm{div} \bm{E}$ を与えます．

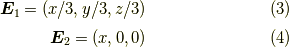
$\bm{E}_1 = (x/3,y/3,z/3) \tag{3} \\\bm{E}_2 = (x,0,0) \tag{4}$

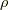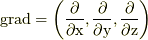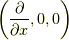よって，ダイバージェンスの値(式(1))だけを与えられても，数学的には，電場を復元できません．しかし，電磁気学ではある前提を課して，電場を一意に復元できます．それは，ずばり式(2)です．ここで，電荷 $\rho$ をデルタ関数とした時を考えると，電場は等方的に広がります．その重ね合わせで，一般の静電場は表現されます．つまり，点電荷からでる電場は等方的であると言う前提があって初めて電場は決定されるのです．今回は式(2)を別の演算子 $\rm{grad}= \left( \dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z} \right)$ から $\left( \dfrac{\partial}{\partial x},0,0 \right)$ に置き換えて，その解の変化を見てみることにします．

式(1)に式(2)の 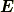$\bm{E}$ を代入すると，電荷とポテンシャルの関係が得られます．それは，

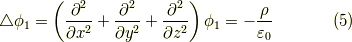
$\triangle \phi_1 = \left( \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial^2}{\partial y^2} + \dfrac{\partial^2}{\partial z^2} \right) \phi_1 = -\dfrac{\rho}{\varepsilon_0} \tag{5}$

と言う関係です．これを 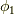$\phi_1$ について解くと，グリーン関数（ここでは単位荷電粒子のポテンシャルと同義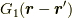） $G_1(\bm{r}-\bm{r}^\prime)$ が次の様に求まります．少々面倒な計算ですが，よく議論されることなので，ここでは求め方は書きません．

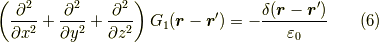
$\left( \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial^2}{\partial y^2} + \dfrac{\partial^2}{\partial z^2} \right) G_1(\bm{r}-\bm{r}^\prime) = -\dfrac{\delta(\bm{r}-\bm{r}^\prime)}{\varepsilon_0} \tag{6}$

が 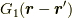$G_1(\bm{r}-\bm{r}^\prime)$ の定義で，

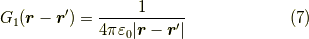
$G_1(\bm{r}-\bm{r}^\prime) = \dfrac{1}{4 \pi \varepsilon_0 |\bm{r}-\bm{r}^\prime|} \tag{7}$

と計算され，

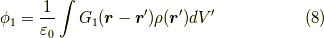
$\phi_1 = \dfrac{1}{\varepsilon_0} \int G_1(\bm{r}-\bm{r}^\prime) \rho(\bm{r}^\prime) dV^\prime \tag{8}$

とポテンシャルを求めるのに使えます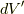． $dV^\prime$ とプライムがつくのは，上の式で積分変数が 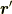$\bm{r}^\prime$ についてのものであるからです．

では，ここで非等方的な電場の出方をするように，式(2)を書き換えてみます．

例えば，

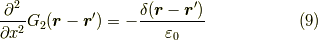
$\dfrac{\partial^2}{\partial x^2} G_2(\bm{r}-\bm{r}^\prime) = -\dfrac{\delta(\bm{r}-\bm{r}^\prime)}{\varepsilon_0} \tag{9}$

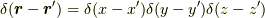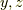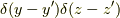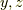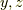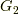これから，超関数の概念をかなり大ざっぱに使います． $\delta(\bm{r}-\bm{r}^\prime)=\delta(x-x^\prime)\delta(y-y^\prime)\delta(z-z^\prime)$ ですので，これは， y,z 平面内では原点に局在するデルタ関数 $\delta(y-y^\prime)\delta(z-z^\prime)$ となります．最初，式(9)は y,z に依存しないと思ったのですが，kuhcrowさんからご指摘いただきまして，そうだ，右辺にデルタ関数として y,z の式が入ってるんだ．と分かりました．一方，軸方向を考えると，これは一次元の問題となり， G_2 の二回微分がデルタ関数，一階微分がシータ関数（階段関数），つまり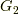， G_2 はランプ関数です．つまり，この世界では電気力線は源泉となる電荷からただ一方ｘ軸の正の方向へ出ていきます．シータ関数 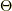$\Theta$ やランプ関数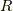とはマイナーな概念化も知れないと思うので，一応書いておきましょう．

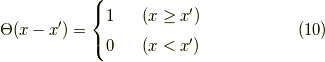
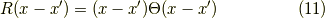
$\Theta(x-x^\prime) = \begin{cases} 1 \ \ \ \ \ (x \geq x^\prime) \\ 0 \ \ \ \ \ (x < x^\prime) \\\end{cases} \tag{10}$ $R(x-x^\prime) = (x-x^\prime) \Theta(x-x^\prime) \tag{11}$

つまり，ランプ関数は式(9)の左辺のラプラシアンで曲率を調べていくと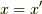， $x=x^\prime$ の点で曲率が発散する関数です．よって，式(6)の代わりに式(9)を採用した世界では，グリーン関数（単位のポテンシャル）は，

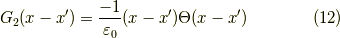
$G_2(x-x^\prime) = \dfrac{-1}{\varepsilon_0}(x-x^\prime)\Theta(x-x^\prime) \tag{12}$

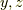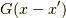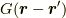となります． y,z 方向も考えて式(7)と対応させるなら， $G(x-x^\prime)$ を $G(\bm{r}-\bm{r}^\prime)$ として，

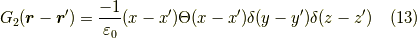
$G_2(\bm{r}-\bm{r}^\prime) = \dfrac{-1}{\varepsilon_0}(x-x^\prime)\Theta(x-x^\prime)\delta(y-y^\prime)\delta(z-z^\prime) \tag{13}$

とすれば比較できるでしょうか．

この式(12)も（簡単のため，本来は式(13)を用いて 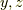y,z 成分はデルタ関数 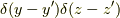$\delta(y-y^\prime)\delta(z-z^\prime)$ を掛けた修正が必要ですが，省略します．）確かにグリーン関数の資格がありますので，式(8)を適用してポテンシャルが求まります．やってみましょう．

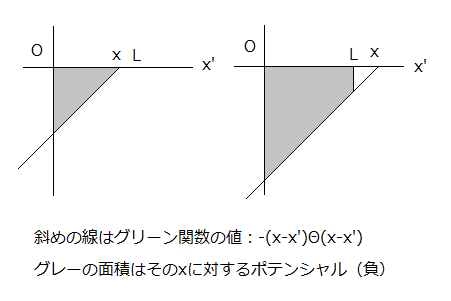
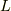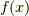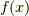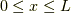原点からx軸の正の方向にの長さに渡って，この非等方な電場を放射する電荷密度 f(x) があるとします．つまり， f(x) を $0 \leq x \leq L$ だけ１，他はゼロを取る関数とします．

以下のような X軸上の一部だけに存在する非等方な電荷密度があるとします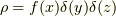．（ $\rho=f(x) \delta(y) \delta(z)$ ）ここで f(x) は x=[0,L]だけ１，他はゼロを取る関数とします．式(8)より，

$\phi_2 &= \int_{-\infty}^{\infty}G_2(x-x^\prime) f(x^\prime)dx^\prime \\&= \dfrac{1}{\varepsilon_0}\int_0^L -( x-x^\prime )\Theta( x-x^\prime ) dx^\prime \\&= \dfrac{1}{\varepsilon_0} \begin{cases}\int_0^x -(x-x^\prime) dx^\prime \ \ \ \ \ (x \leq L) \\\int_0^L -(x-x^\prime) dx^\prime \ \ \ \ \ (x > L)\end{cases} \\&= \dfrac{1}{\varepsilon_0} \begin{cases}\left[ \dfrac{(x^\prime-x)^2}{2} \right]_0^x \ \ \ \ \ (x \leq L) \\\left[ \dfrac{(x^\prime-x)^2}{2} \right]_0^L \ \ \ \ \ (x > L)\end{cases} \\&= \dfrac{1}{\varepsilon_0} \begin{cases}-\dfrac{x^2}{2} \ \ \ \ \ (x \leq L) \\- xL + \dfrac{L^2}{2} (x > L)\end{cases} \tag{14}$

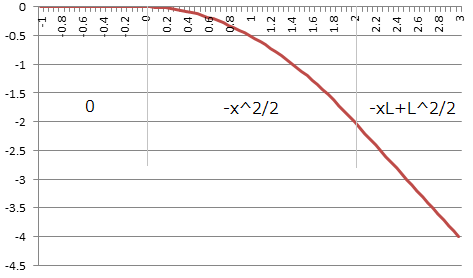
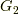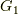これが非等方な電場を放射する電荷密度を持つポテンシャルの例です．この電場のポテンシャルは右に行くとどんなに遠くでも無限に（負で）大きくなりますが，これの G_2 が G_1 だと，定性的に述べると十分遠くからだと，点電荷に近くなり 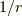1/r 則で減衰し，無限遠でポテンシャルはゼロとなります．全く異なる振る舞いになりますね．

今回の教訓は，同じ 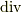$\rm{div}$ を持つ関数でも，数学的には異なるベクトル場（電場）を表すことがある．一方，物理（電磁気学）的には異なるベクトル場（電場）は排除され，ただ一通りに決まる．というのは，ここで見た通りです．よろしいですか？式(7)も式(13)もそれぞれ

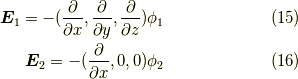
$\bm{E}_1 = -(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z})\phi_1 \tag{15} \\\bm{E}_2 = -(\dfrac{\partial}{\partial x},0,0)\phi_2 \tag{16}$

という異なる法則に従っていますが，同じダイバージェンス

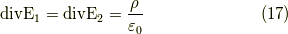
$\rm{div} \bm{E}_1 = \rm{div} \bm{E}_2 = \dfrac{\rho}{\varepsilon_0} \tag{17}$

に従っているよ．と言うお話です．最後に何故 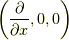$\left( \dfrac{\partial}{\partial x},0,0 \right)$ を取ったか．実はこれは話の順序が逆で，まず最初に電場がポテンシャルからx軸方向の一方に伸びる関数を考えました．それについて考えていたら，偶然 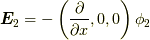$\bm{E}_2 = -\left( \dfrac{\partial}{\partial x},0,0 \right) \phi_2$ と言う尤もらしい微分演算子が見つかったと言うわけです．今日はここまで，お疲れ様でした．

[home] [電磁気学] [ページの先頭]