この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
平行移動,回転,時間発展とポアソン括弧
ハミルトニアンは時間発展,運動量は平行移動,角運動量は回転と関係していると聞いたことはありませんか? 僕が知っていたのは,ネーターの定理あたりの話からだったのですが, ポアソン括弧を使ってもっと直接的関係が得られることに気づきました. 量子力学では有名な話です.ただ,私はその古典力学での対応を知りませんでした. この記事は証明と言うよりは,検証・確認です.
ポアソン括弧
ポアソン括弧とは,運動量 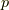 ,位置
,位置 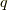 ,時間
,時間  と正準変数の関数
と正準変数の関数 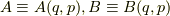 を用いた,
を用いた,
![[A,B] = \dfrac{\partial A}{\partial q}\dfrac{\partial B}{\partial p} -\dfrac{\partial A}{\partial p}\dfrac{\partial B}{\partial q} \tag{1}](http://hooktail.maxwell.jp/kagi/bfb3c39d4df084a7a13ec2335619c637.png)
と言う計算の事です.
時間発展とハミルトニアン
これは有名だと思います.関数 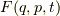 の時間発展は,ハミルトニアン
の時間発展は,ハミルトニアン 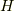 を用いて,
を用いて,
![\dfrac{d}{dt}F(q,p,t) = [F,H] + \dfrac{\partial F}{\partial t} \tag{2}](http://hooktail.maxwell.jp/kagi/2c255e03b33f5e1a5f537a4e8e3fe468.png)
という方程式になります.特に 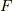 が時間を陽に含まない時,
が時間を陽に含まない時,
![\dfrac{d}{dt}F(q,p) = [F,H] \tag{3}](http://hooktail.maxwell.jp/kagi/e55b41866afbda99d1f7e7eeb62bfbee.png)
となります.試しに
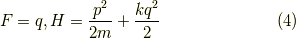
として式を計算すると,
![\dfrac{dq}{dt} &= [q,\dfrac{p^2}{2m}+\dfrac{kq^2}{2}] \\&= \dfrac{\partial q}{\partial q}\dfrac{\partial \left( \dfrac{p^2}{2m}+\dfrac{kq^2}{2} \right)}{\partial p} -\dfrac{\partial q}{\partial p}\dfrac{\partial \left( \dfrac{p^2}{2m}+\dfrac{kq^2}{2} \right)}{\partial q} \\&= p/m \tag{5}](http://hooktail.maxwell.jp/kagi/a61feb5da745d317f6a0a8919b84cfb2.png)
となり,確かに正しい運動方程式です. 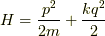 としたハミルトン方程式
としたハミルトン方程式

と等価です.
平行移動と運動量
式 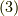 に対応させて以下の式を考えてみました.
に対応させて以下の式を考えてみました.
![\dfrac{d}{dq}F(q,p) = [F(q,p),p] \tag{6}](http://hooktail.maxwell.jp/kagi/64dbcf8521a4501c19d64c5eec4136b8.png)
右辺を計算すると,
![[F(q,p),p] = \dfrac{\partial F}{\partial q}\dfrac{\partial p}{\partial p} -\dfrac{\partial F}{\partial p}\dfrac{\partial p}{\partial q}\tag{7}](http://hooktail.maxwell.jp/kagi/8bf8200d962ac8bd72a9c9c5eb101b90.png)
特に  としてみると,左辺が,
としてみると,左辺が,

であり,右辺が
![[\dfrac{k}{2}q^2,p] &= \dfrac{\partial \left( \dfrac{k}{2}q^2 \right) }{\partial q}\dfrac{\partial p}{\partial p} -\dfrac{\partial \left( \dfrac{k}{2}q^2 \right)}{\partial p}\dfrac{\partial p}{\partial q} \\&= kq](http://hooktail.maxwell.jp/kagi/9e1b21616bcba076922763729493b29d.png)
となり,一致していますね.
回転と角運動量
最後に二次元平面での回転を見ましょう.

ですから,二次元に制限すると, 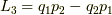 を考えれば良く,
を考えれば良く,
![\dfrac{d}{d \theta}F(q_1,q_2,p_1,p_2) &= \sum_{i} [F,L_3] \\&= \sum_{i} \left( \dfrac{\partial F}{\partial q_i}\dfrac{\partial L_3}{\partial p_i} - \dfrac{\partial F}{\partial p_i}\dfrac{\partial L_3}{\partial q_i} \right)\tag{10}](http://hooktail.maxwell.jp/kagi/555c60fd9fad72cac4eebbd2e67887dd.png)
です. 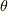 は回転角です.例えば,
は回転角です.例えば,
![[F(q_1,q_2,p_1,p_2),L_3] &= \dfrac{\partial F}{\partial q_1}\dfrac{\partial L_3}{\partial p_1} -\dfrac{\partial F}{\partial p_1}\dfrac{\partial L_3}{\partial q_1} + \dfrac{\partial F}{\partial q_2}\dfrac{\partial L_3}{\partial p_2} -\dfrac{\partial F}{\partial p_2}\dfrac{\partial L_3}{\partial q_2} \\&= \dfrac{\partial F}{\partial q_1} \cdot (-q_2) - \dfrac{\partial F}{\partial p_1} \cdot p_2 + \dfrac{\partial F}{\partial q_2} \cdot q_1 - \dfrac{\partial F}{\partial p_2} \cdot (-p_1)\tag{11}](http://hooktail.maxwell.jp/kagi/495a3d769aa28357657af7ccccdb6224.png)
となります.ここで, 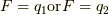 とすると,
とすると,
![\dfrac{d q_1}{d \theta} &= [q_1,L_3] = -q_2 \\\dfrac{d q_2}{d \theta} &= [q_2,L_3] = q_1 \tag{12}](http://hooktail.maxwell.jp/kagi/ebc7d4b5c7c0945ab0c785b5b60e050d.png)
はて,これはどうしたらいいでしょう? 行列を使って書き直してみましょう.
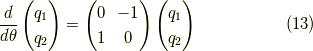
となり,行列の指数関数を使えば良さそうです. 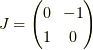 として,
解くと,
として,
解くと,
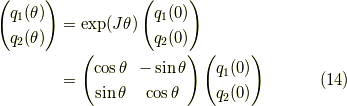
となりました.これは正に(能動的)回転の行列ですね.
それでは,今日はこの辺で.お疲れ様でした.