この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
テイラー級数
「テイラー展開すると…」なんて言葉が教科書によく出てきます. これはテイラー級数で表す,という意味で使われています. その頻出するテイラー級数を,簡単に紹介します.
テイラー級数
つぎの無限級数
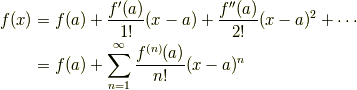
を関数 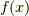 の
の 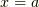 におけるテイラー級数といいます.
におけるテイラー級数といいます.
マクローリン級数
主に有限の 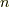 で展開を止めて近似式として用います.
たいていは1次か2次程度で近似します.テイラー級数で
で展開を止めて近似式として用います.
たいていは1次か2次程度で近似します.テイラー級数で 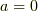 のもの,すなわち
のもの,すなわち
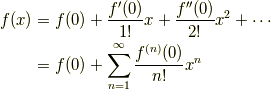
をマクローリン級数といいます.でも単にテイラー級数と言った場合も, このマクローリン級数を指すことが多いようです.
例
例として, 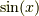 の
の 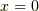 でのテイラー級数(マクローリン級数)を見てみます.
素直に公式に当てはめると
でのテイラー級数(マクローリン級数)を見てみます.
素直に公式に当てはめると
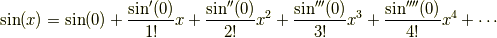
ここで
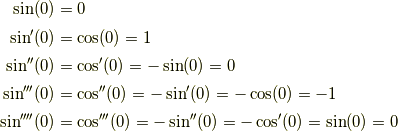
ですから,
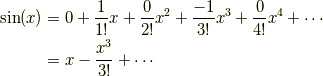
となります. 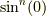 の微分を繰り返すと分かるように,
この先もずうっと偶数番目の項は消え,
奇数番目の項がプラスマイナスを繰り返しながら残るので,結局
の微分を繰り返すと分かるように,
この先もずうっと偶数番目の項は消え,
奇数番目の項がプラスマイナスを繰り返しながら残るので,結局
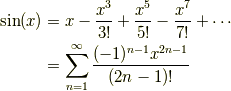
となります.この右辺のように数列の無限個の和で表されるものを「べき級数」と呼びます.
この例で 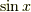 をべき級数に変形したように,
ある関数をべき級数で表すことを「べき級数展開」と呼びます.
をべき級数に変形したように,
ある関数をべき級数で表すことを「べき級数展開」と呼びます.
もう一つ
また,物理では
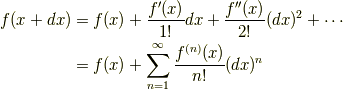
というテイラー級数も良く使われます.