この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ホッジ作用素
外積空間 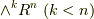 について,その次元は
について,その次元は 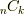 になるのでした.ここで,二項係数
になるのでした.ここで,二項係数 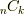 について,
について, 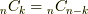 が成り立つことに気がついた人がいると思います.具体的には,
が成り立つことに気がついた人がいると思います.具体的には, 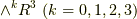 ならば,
ならば, 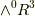 の次元と
の次元と 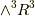 の次元が同じ(基底はそれぞれ
の次元が同じ(基底はそれぞれ 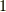 と
と 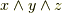 で,どちらも一次元),
で,どちらも一次元), 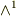 の次元と
の次元と 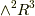 の次元が同じ(基底はそれぞれ
の次元が同じ(基底はそれぞれ 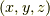 と
と 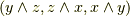 で三次元)になっています.これは,二項係数の分布が対称だということの結果です.二項係数は,次図のパスカルの三角形と呼ばれる形に配列すると綺麗にその対称性が分かります.(上から四段目が,
で三次元)になっています.これは,二項係数の分布が対称だということの結果です.二項係数は,次図のパスカルの三角形と呼ばれる形に配列すると綺麗にその対称性が分かります.(上から四段目が, 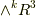 の次元を表わしています.)
の次元を表わしています.)
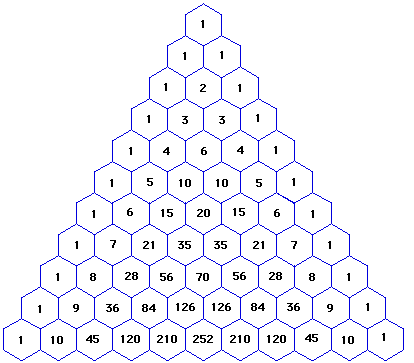
二項係数の分布は左右対称だ.(図は MathForum@Drexel 様から許可を得て頂きました.有難うございました.)
逆に言えば,ある 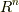 から生成される外積代数で,
から生成される外積代数で, 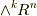 と同じ次元の外積空間は
と同じ次元の外積空間は 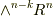 しか無いことが分かります.(これは
しか無いことが分かります.(これは 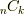 の性質を考えてみれば明らかです.)パスカルの三角形の対称性を見たら, 右半分と左半分をぜひ対応させてみたい と思うのが人情ですよね.いかにも一対一に対応しそうですから.(え?そんなこと思わないって??)そこで,『次元
の性質を考えてみれば明らかです.)パスカルの三角形の対称性を見たら, 右半分と左半分をぜひ対応させてみたい と思うのが人情ですよね.いかにも一対一に対応しそうですから.(え?そんなこと思わないって??)そこで,『次元 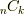 の外積空間と,次元
の外積空間と,次元  の外積空間を一対一に対応させる写像』を考えてみようとアイデアが出てくると思います.ホッジ作用素とは,そんな写像です.
の外積空間を一対一に対応させる写像』を考えてみようとアイデアが出てくると思います.ホッジ作用素とは,そんな写像です.
ウェッジ積を考える
まず,先ほどの序文で『次元が同じなら,対応させてみよう』と考えていた,二つの外積空間 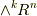 と
と 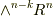 から一つずつ元を選び,そのウェッジ積を考えてみます.
から一つずつ元を選び,そのウェッジ積を考えてみます.
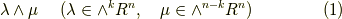
ここで, ウェッジ積について補足 で紹介したように,一般にウェッジ積と元の次数について, 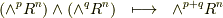 が成り立ちますので,このウェッジ積は
が成り立ちますので,このウェッジ積は 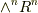 の元になります.
の元になります. 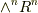 は一次元のベクトル空間ですから,独立な基底は一個しかありません.この基底を
は一次元のベクトル空間ですから,独立な基底は一個しかありません.この基底を 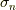 とします.
とします. 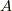 を適切なスカラーとして,式
を適切なスカラーとして,式 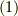 は次のように表現できるでしょう.(ちょっと変な記法ですが,
は次のように表現できるでしょう.(ちょっと変な記法ですが,  の右下の添字は,外積空間の階数を表わすものとします.)
の右下の添字は,外積空間の階数を表わすものとします.)
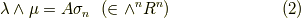
スカラー 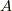 は,
は,  と
と 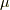 によって一意的に決まるはずです.そのことを念頭に置きつつ,式
によって一意的に決まるはずです.そのことを念頭に置きつつ,式 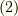 のウェッジ積を少し違う角度で見てみます.『
のウェッジ積を少し違う角度で見てみます.『 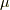 が変数で,
が変数で, 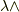 は線形汎関数であり,それによって
は線形汎関数であり,それによって 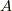 が表現される』と見るのです.(まったく同じ見方を,既に 内積と双対空間 で用いています.復習してみて下さい.)
が表現される』と見るのです.(まったく同じ見方を,既に 内積と双対空間 で用いています.復習してみて下さい.) 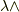 が線形汎関数だということを見やすくするために,
が線形汎関数だということを見やすくするために, 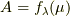 と書いても良いでしょう.
と書いても良いでしょう.

| [*] | こんな見方が出来るのは,わざと  と と 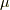 の階数を の階数を 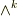 と と 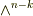 に選んだからです.逆に言えば,線形汎関数という見方を使いたくて,最初からを に選んだからです.逆に言えば,線形汎関数という見方を使いたくて,最初からを 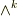 と と 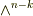 のウェッジ積を考えたりしてるんです. のウェッジ積を考えたりしてるんです.  ( ( 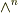 は一次元!)という形の一次変換を作りたかったのでした. は一次元!)という形の一次変換を作りたかったのでした. |
何だか,色々なことを書きましたが,式 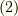 と式
と式 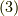 は,何も式を発展させてませんので同じ式のままです.ただ,ちょっと見方を変え,表記を変えてみただけです.(しかし,視点の変更はいつでも面白いものです.)
は,何も式を発展させてませんので同じ式のままです.ただ,ちょっと見方を変え,表記を変えてみただけです.(しかし,視点の変更はいつでも面白いものです.)
内積を対応させる
ここで, p-ベクトルの内積 の記事の最後の定理を使うと,『線形汎関数は内積を使って一意的に表わすことができる』ということでした.つまり,式 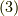 の線形汎関数を,次式のように一意的に内積で表現する元
の線形汎関数を,次式のように一意的に内積で表現する元  が,
が, 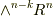 中に(つまり
中に(つまり 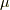 と同じベクトル空間内に)必ず存在するというのです.
と同じベクトル空間内に)必ず存在するというのです.
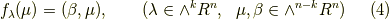
そろそろ,予め内積を勉強しておいたことや,前セクションで話を線形汎関数に持っていったことの意図が明らかになってきたと思います.この 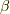 は,線形汎関数
は,線形汎関数 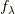 を内積の形で代弁しているのであって,
を内積の形で代弁しているのであって,  によって一意的に決まる元のはずですから,
によって一意的に決まる元のはずですから, 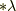 と書くことにします.すると,式
と書くことにします.すると,式 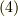 を式
を式 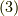 に代入し,
に代入し, 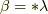 と書くことで次式を得ます.(内積は,同じ外積空間の二つの元に対して考えるのでしたから,
と書くことで次式を得ます.(内積は,同じ外積空間の二つの元に対して考えるのでしたから, 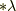 は
は 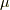 と同じく
と同じく 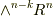 の元です.
の元です.  は
は 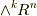 の元です.しっかり頭を整理しながら読んで下さい.)
の元です.しっかり頭を整理しながら読んで下さい.)

こんな変形が可能であったのも,  と
と 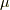 の階数が,足したら
の階数が,足したら  になるという特殊なものであったからだという点を再確認して下さい.
になるという特殊なものであったからだという点を再確認して下さい.  は
は 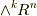 の元ですが,
の元ですが, 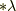 は
は 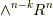 の元です.この星印を ホッジ作用素 (もしくは, ホッジのスター作用素 , ホッジの星印作用素 , ホッジスター など)と呼びます.ホッジ作用素を取るという操作は,確かに
の元です.この星印を ホッジ作用素 (もしくは, ホッジのスター作用素 , ホッジの星印作用素 , ホッジスター など)と呼びます.ホッジ作用素を取るという操作は,確かに 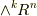 から
から 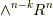 への写像になっています.これは,序文で考えていた狙い通りです.
への写像になっています.これは,序文で考えていた狙い通りです.
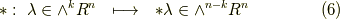
蛇足ですが,あるベクトル空間に対し,その線形汎関数の集合を双対空間と呼ぶのでした. 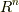 や外積空間
や外積空間 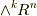 には内積が定義されていますので,ここまでの議論により,次のことが言えます.( 双対基底と双対空間 参照.)
には内積が定義されていますので,ここまでの議論により,次のことが言えます.( 双対基底と双対空間 参照.)
Important
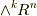 と
と 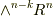 は,互いに双対空間になっている.
は,互いに双対空間になっている.
外積代数の美しい構造がだんだん見えて来ましたね.
| [†] | 最初に掲げたパスカルの三角形の図で,  段目の数字 段目の数字 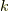 を を 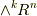 に対応させることにすると(ただし一番上を零段目とします),この三角形の左半分と右半分で表わされる空間が,それぞれ双対空間になっていると言えそうです.三角形の左右対称という構造と,双対という構造がここで重なってきました.美しいです. に対応させることにすると(ただし一番上を零段目とします),この三角形の左半分と右半分で表わされる空間が,それぞれ双対空間になっていると言えそうです.三角形の左右対称という構造と,双対という構造がここで重なってきました.美しいです. |
基底や空間の向きに注意する
ここまでで, 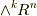 から
から 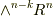 の写像としてのホッジ作用素の骨格は与えられました.考えてみれば,
の写像としてのホッジ作用素の骨格は与えられました.考えてみれば, 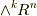 と
と 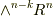 は次元が等しいベクトル空間なのですから,この二つを結ぶ同型写像が存在するであろうことは察しのつくことで,ホッジ作用素はまさにそのような同型写像の一つなのです.
は次元が等しいベクトル空間なのですから,この二つを結ぶ同型写像が存在するであろうことは察しのつくことで,ホッジ作用素はまさにそのような同型写像の一つなのです.
しかし,ホッジ作用素の定義はこれで全部ではありません.少し細かいことのように思うかも知れませんが,基底の向きを決めて置かなければなりません.(式 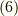 は定義であって,また実用的な表現にはなっていません.ホッジ作用素の写像も具体的に決めるまでに,まだ説明しなければなたないことが幾つかあるのです.少し長丁場になりますが,頑張って下さいo(>_<)o)
は定義であって,また実用的な表現にはなっていません.ホッジ作用素の写像も具体的に決めるまでに,まだ説明しなければなたないことが幾つかあるのです.少し長丁場になりますが,頑張って下さいo(>_<)o)
| [‡] | 例えば,もし 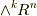 の元 の元  を を 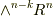 の元 の元 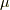 に移す同型写像があれば, に移す同型写像があれば,  を を 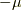 に移す写像もあるはずです.これを区別するには,やはり基底の並び方や符号の問題をきちんと整理しておく必要があります.少し煩雑な感じがしますが,今後のために重要な問題です. に移す写像もあるはずです.これを区別するには,やはり基底の並び方や符号の問題をきちんと整理しておく必要があります.少し煩雑な感じがしますが,今後のために重要な問題です. |
まずベクトル空間 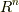 の向きを決める
の向きを決める
まず最初に,ベクトル空間 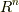 に『向き』をつけます.『空間の向き』とは何のことか,聞き慣れない人もいるかも知れませんが,ある独立な一組の基底を決めて順番に並べ,
に『向き』をつけます.『空間の向き』とは何のことか,聞き慣れない人もいるかも知れませんが,ある独立な一組の基底を決めて順番に並べ, 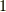 から
から  まで番号を振り,その基底(必ずしも直交基底である必要はありません)を, 空間の向き と定めることにするのです.例えば,次のように基底を並べ,これを
まで番号を振り,その基底(必ずしも直交基底である必要はありません)を, 空間の向き と定めることにするのです.例えば,次のように基底を並べ,これを 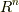 の向きと決めます.(向きとは『基底を並べたもの』のことです.日常用語の感覚からは,少し意味に違和感を覚えるかも知れません.)
の向きと決めます.(向きとは『基底を並べたもの』のことです.日常用語の感覚からは,少し意味に違和感を覚えるかも知れません.)

これ以外の基底(例えば 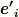 )は,この基底に行列を作用させた形
)は,この基底に行列を作用させた形 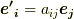 で表現できますが,この変換を表わす行列
で表現できますが,この変換を表わす行列 ![[a_{ij}]](http://hooktail.maxwell.jp/kagi/78db614e8d60af195d78d8bbe9f3d895.png) の行列式の符号に応じて,新しい基底に従う空間の向きを
の行列式の符号に応じて,新しい基底に従う空間の向きを 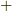 とか
とか  と決めることにします.そして特に,行列式が正の行列による変換で表わせる基底以外を考えないとき, ベクトル空間に向きをつけた と言います.ひとたび
と決めることにします.そして特に,行列式が正の行列による変換で表わせる基底以外を考えないとき, ベクトル空間に向きをつけた と言います.ひとたび 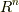 に向きが決まると,
に向きが決まると, 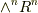 の基底を決めることができます.式
の基底を決めることができます.式 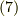 の順番のまま,間にウェッジ積を挟んで結合したものを,
の順番のまま,間にウェッジ積を挟んで結合したものを, 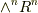 の正規直交基底と決めるのが自然です.
の正規直交基底と決めるのが自然です.
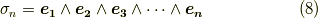
つまり,式 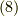 の基底に対し
の基底に対し 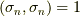 と決める訳です.(
と決める訳です.( 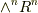 は一次元ですから,必ず
は一次元ですから,必ず 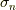 を
を 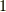 に対応させる写像は存在するはずです.このように決めてしまおうということです.)このような操作を, 空間の向きを決める と言います.
に対応させる写像は存在するはずです.このように決めてしまおうということです.)このような操作を, 空間の向きを決める と言います.
| [§] | 外積空間  の非零な基底をボリューム・フォームと呼びます. の非零な基底をボリューム・フォームと呼びます. 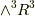 の場合に,基底が体積素を意味することからついた名前なのでしょう.先ほどは の場合に,基底が体積素を意味することからついた名前なのでしょう.先ほどは 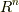 の基底の並べ方を決めてからボリューム・フォームを決めましたが,先に の基底の並べ方を決めてからボリューム・フォームを決めましたが,先に 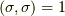 と,ボリュームフォームの内積の符号を決めることで空間に向きを付けても良いでしょう.むしろ,後者の方が手間が少ないので,馴れている人はいきなりボリュームフォームを書きます. と,ボリュームフォームの内積の符号を決めることで空間に向きを付けても良いでしょう.むしろ,後者の方が手間が少ないので,馴れている人はいきなりボリュームフォームを書きます. |
ウェッジ積の性質より,式 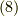 で,どこか隣り合った基底の並びを交換すると,
で,どこか隣り合った基底の並びを交換すると, 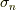 の符号が変わります.
の符号が変わります.
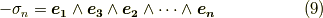
この性質は,実は,右手系⇔左手系の取り方を逆にすると,ベクトルの外積( 軸性ベクトル )や スカラー三重積 によって表わされた平行六面体の体積の符号が逆になる,という現象として,既に知っているものです.式 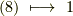 のようにして空間の向きを決める手続きは,右手系か左手系かを決めることと同じなのです.もちろん,三次元ユークリッド空間以外では『右手の親指,人差し指,中指を開いて,こっちが右手系』などという直観的定義は無意味ですが,『ボリュームフォームを
のようにして空間の向きを決める手続きは,右手系か左手系かを決めることと同じなのです.もちろん,三次元ユークリッド空間以外では『右手の親指,人差し指,中指を開いて,こっちが右手系』などという直観的定義は無意味ですが,『ボリュームフォームを 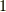 とするのが右手系』『ボリュームフォームを
とするのが右手系』『ボリュームフォームを 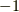 とするのが左手系』と決めれば,これは三次元ユークリッド空間の右手系・左手系を自然に拡張したものになります.
とするのが左手系』と決めれば,これは三次元ユークリッド空間の右手系・左手系を自然に拡張したものになります.
基底のウェッジ積だけ考えてみる
もう一度 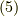 式を考えます.(再掲します.)
式を考えます.(再掲します.)

ここで特に,  として
として 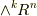 の基底
の基底 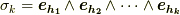 を考え,
を考え, 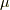 として,特に
として,特に 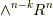 の基底
の基底 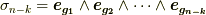 を考えてみましょう.(ただし,
を考えてみましょう.(ただし, 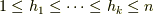 ,
, 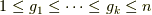 とします.)
とします.)
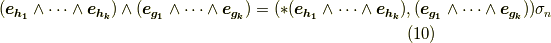
もし 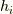 と
と 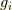 の中に重複するものが一つでもあれば,ウェッジ積の性質より式
の中に重複するものが一つでもあれば,ウェッジ積の性質より式 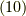 の左辺は
の左辺は 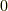 になってしまいますので,左辺を
になってしまいますので,左辺を 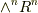 の一つの元と対応させるためには,
の一つの元と対応させるためには, 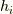 と
と 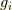 が,過不足無く,
が,過不足無く, 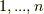 を
を 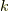 個の
個の 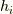 と
と  個の
個の 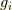 に分ける場合に限ることが分かります.そこで,新たに
に分ける場合に限ることが分かります.そこで,新たに 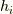 と
と 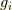 を合わせて
を合わせて 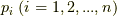 と置くと,次のように書けます.つまり,
と置くと,次のように書けます.つまり, 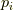 は
は  を並べ替えた順列です.
を並べ替えた順列です.
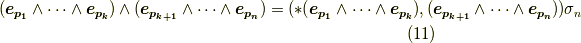
一方,式 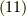 の左辺は,単に
の左辺は,単に 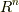 の基底の積なので,(ホッジ演算子などと関係なく単なるウェッジ積として)次のように書けます.
の基底の積なので,(ホッジ演算子などと関係なく単なるウェッジ積として)次のように書けます.
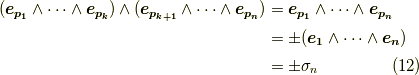
式 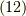 の右辺の符号は,前セクションで考えた,空間の向きに関する議論より『
の右辺の符号は,前セクションで考えた,空間の向きに関する議論より『 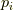 が
が  の偶置換ならば
の偶置換ならば 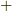 ,奇置換ならば
,奇置換ならば  』だと決められることが分かります.この
』だと決められることが分かります.この 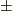 の符号は,置換記号
の符号は,置換記号 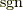 を用いて,次のように表記しておくことにします.
を用いて,次のように表記しておくことにします.
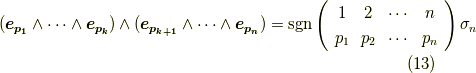
次にやることは式  と式
と式 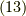 の比較ですが, p-ベクトルの内積 で考えたように,一般的には,p-ベクトルの内積の符号がもう一つの問題になってきます.
の比較ですが, p-ベクトルの内積 で考えたように,一般的には,p-ベクトルの内積の符号がもう一つの問題になってきます.
空間の符号定数
最初に,空間の向きが保たれている状態(つまり右手系は右手系に,左手系は左手系に移される状態)を考えましょう.すると,前セクションで考えた  は常に
は常に  となりますので,式
となりますので,式 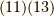 を比べて次式を得ます.
を比べて次式を得ます.
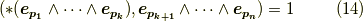
ここで, 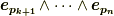 自身の内積
自身の内積 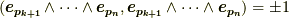 と比較すると,ホッジ作用素について次式が言えます.
と比較すると,ホッジ作用素について次式が言えます.
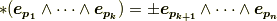
またしても,面倒なことに 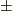 がついています.ここで,
がついています.ここで, 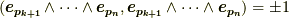 の符号が
の符号が  になるのは,基底
になるのは,基底  の中に,計量が負であるもの(例えばミンコフスキー空間の時間軸)が奇数個ある場合です.( p-ベクトルの内積 の最後のセクションを参照して下さい.) 基底
の中に,計量が負であるもの(例えばミンコフスキー空間の時間軸)が奇数個ある場合です.( p-ベクトルの内積 の最後のセクションを参照して下さい.) 基底  の中に,計量を負とするものが偶数個(
の中に,計量を負とするものが偶数個( 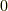 個も偶数)ある場合は,右辺の符号は
個も偶数)ある場合は,右辺の符号は 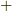 になります.
になります.  に含まれる『計量が負である基底の数』を
に含まれる『計量が負である基底の数』を  として,式
として,式 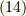 と前セクションの議論より,ホッジ作用素のついて最終的に次のことが言えます.
と前セクションの議論より,ホッジ作用素のついて最終的に次のことが言えます.
【空間の向き(右手・左手系)が保たれ,  が偶数の場合】
が偶数の場合】

【空間の向き(右手・左手系)が保たれ,  が奇数の場合】
が奇数の場合】
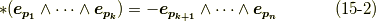
【空間の向き(右手・左手系)が変わり,  が偶数の場合】
が偶数の場合】
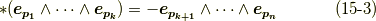
【空間の向き(右手・左手系)が変わり,  が奇数の場合】
が奇数の場合】
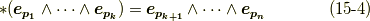
符号の話が随分面倒でしたが,『空間の向き』という話と,『計量が負になるような基底が幾つあるか』という話が二種類絡んで来ているという点を確認して下さい.式 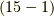 はとても明快な形をしてますので,ひとまず式
はとても明快な形をしてますので,ひとまず式 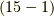 を覚えておいて,空間の向きや符号定数を考えて符号に注意するようにすれば良いと思います.抽象的な議論が続いたので,長い道のりに感じたかも知れませんが,次セクションの具体例を見れば,ホッジ演算子が直観的に理解し易い概念であることが分かると思います.ここまでの議論をまとめます.
を覚えておいて,空間の向きや符号定数を考えて符号に注意するようにすれば良いと思います.抽象的な議論が続いたので,長い道のりに感じたかも知れませんが,次セクションの具体例を見れば,ホッジ演算子が直観的に理解し易い概念であることが分かると思います.ここまでの議論をまとめます.
definition
【ホッジ作用素】ベクトル空間 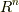 の基底を
の基底を 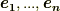 とし,
とし, 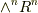 のボリュームフォームを
のボリュームフォームを  と決めます.
と決めます. 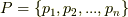 は
は  の順列として,次のような
の順列として,次のような 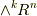 から
から  への写像をホッジ作用素と定義し,*で表わします.
への写像をホッジ作用素と定義し,*で表わします.  ただし,
ただし,  は
は 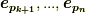 中にある,計量を負とする基底の数とします.
中にある,計量を負とする基底の数とします.
| [¶] | 『計量を負とする基底の数』が問題になっているのは, 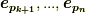 の中にそのような基底が幾つ含まれるかだけである点に注意して下さい.つまり, の中にそのような基底が幾つ含まれるかだけである点に注意して下さい.つまり, 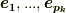 の中に幾つ含まれていようと,符号には関係しません.『空間の向き』と『計量を負とする基底の数』という二つの話が一緒になっているので,符号の話をかなり面倒に感じていると思いますが,ここは大事なところなのでしっかり理解しておいて下さい.実際に計算する場合には,『空間の向きは保つ』と決めてしまって,右手系⇔左手系を入れ替えるような操作を考慮しないことが多いですし,計量が負になる基底が出て来るのも,まずはミンコフスキー空間だけですので,そんなに難しくはありません. ミンコフスキー空間上の微分形式 で,ミンコフスキー空間上でのホッジ作用素を使います. の中に幾つ含まれていようと,符号には関係しません.『空間の向き』と『計量を負とする基底の数』という二つの話が一緒になっているので,符号の話をかなり面倒に感じていると思いますが,ここは大事なところなのでしっかり理解しておいて下さい.実際に計算する場合には,『空間の向きは保つ』と決めてしまって,右手系⇔左手系を入れ替えるような操作を考慮しないことが多いですし,計量が負になる基底が出て来るのも,まずはミンコフスキー空間だけですので,そんなに難しくはありません. ミンコフスキー空間上の微分形式 で,ミンコフスキー空間上でのホッジ作用素を使います. |
具体例
具体例を,三次元ニュークリッド空間 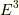 で考えてみます.
で考えてみます. 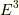 の正規直交基底を
の正規直交基底を 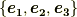 とし,
とし, 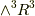 の基底(ボリュームフォーム)を
の基底(ボリュームフォーム)を 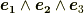 と決めます.このとき,ホッジ作用素は,次のような作用をすることが言えます.
と決めます.このとき,ホッジ作用素は,次のような作用をすることが言えます.
| [#] | いま, 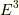 には計量を負とするような基底はありません( には計量を負とするような基底はありません( 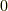 個と言ってもよい)から,符号定数云々といった注意は,ここでは必要ありません.忘れましょう♪ 個と言ってもよい)から,符号定数云々といった注意は,ここでは必要ありません.忘れましょう♪ |






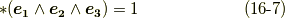
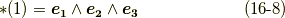
式 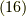 の各式に出て来る添字の並びは,全て
の各式に出て来る添字の並びは,全て 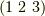 の偶置換であり,だから右辺が全て
の偶置換であり,だから右辺が全て 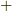 であることを確認して下さい.式
であることを確認して下さい.式 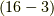 を例に考えてみると,
を例に考えてみると,  をもし
をもし 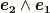 に写像するならば,このとき添字の並び
に写像するならば,このとき添字の並び  は,
は, 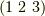 の奇置換ですから,右辺に
の奇置換ですから,右辺に  が必要になります.
が必要になります.

こう書きたければこれでも構いませんが,ウェッジ積の性質 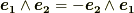 より,結局この式は
より,結局この式は 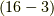 と同じになります.前セクションで,空間の向きをごちゃごちゃ議論したときに『面倒くさいなぁ(@_@) 』と思った人が多いと思いますが,こうやって見てみると,空間の向きに関する注意とウェッジ積の交代性は,うまく辻褄が合っていることに気がつくと思います.
と同じになります.前セクションで,空間の向きをごちゃごちゃ議論したときに『面倒くさいなぁ(@_@) 』と思った人が多いと思いますが,こうやって見てみると,空間の向きに関する注意とウェッジ積の交代性は,うまく辻褄が合っていることに気がつくと思います.
どうでしょう,式 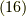 は,意外に分かりやすい結果だと思いませんか?
は,意外に分かりやすい結果だと思いませんか?
具体例の発展
式 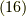 を使って, ウェッジ積について補足 の記事の最後で『ウェッジ積の例』として考えた問題を再び取り上げてみます.
を使って, ウェッジ積について補足 の記事の最後で『ウェッジ積の例』として考えた問題を再び取り上げてみます. 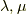 を1-ベクトル(
を1-ベクトル( 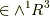 )とすると,次式が成り立ちます.
)とすると,次式が成り立ちます.

両辺の  を取ってみます.
を取ってみます.
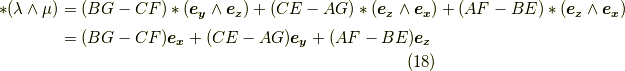
これは・・・,なんとベクトルの外積になっています.いままで『ベクトルの外積』として知っていた計算の正体は,『 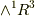 の元のウェッジ積にホッジ作用素を作用させたもの』だったのです.もしも,『ベクトルの外積って,何となくアヤシイ計算だなぁ』と常々感じていた人は,ここで長年の胸のつかえを解消して欲しいところであります.
の元のウェッジ積にホッジ作用素を作用させたもの』だったのです.もしも,『ベクトルの外積って,何となくアヤシイ計算だなぁ』と常々感じていた人は,ここで長年の胸のつかえを解消して欲しいところであります.
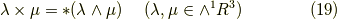
もう一つ,1-ベクトル 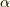 と2-ベクトル
と2-ベクトル 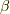 のウェッジ積も考えてみます.
のウェッジ積も考えてみます.
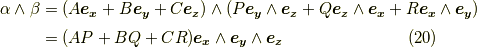
両辺の  を取ってみます.
を取ってみます.
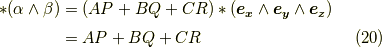
これは『双対ベクトルの内積がスカラーになる』というベクトルの計算を意味しています.( 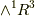 と
と 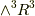 は互いに双対空間になっている事を思い出してください.)これも,ウェッジ積とホッジ作用素で書き換えると次のようになります.
は互いに双対空間になっている事を思い出してください.)これも,ウェッジ積とホッジ作用素で書き換えると次のようになります.
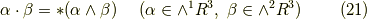
式  は,元の属する空間が違うだけで,式
は,元の属する空間が違うだけで,式  と基本的には同じ形をしていますね.つまり,『ウェッジ積を取ってから,ホッジ作用素を掛ける』という形です.いままで違うものだと思っていたベクトルの演算が,ウェッジ積,ホッジの作用素といった,より高い視点を得たことで,だんだんと統一的に見えて来ました.面白いですね!
と基本的には同じ形をしていますね.つまり,『ウェッジ積を取ってから,ホッジ作用素を掛ける』という形です.いままで違うものだと思っていたベクトルの演算が,ウェッジ積,ホッジの作用素といった,より高い視点を得たことで,だんだんと統一的に見えて来ました.面白いですね!