この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
共役類
集合の元の間に,共役という関係を考えます.共役は同値関係なので,これによって群を類別することができます.この記事では,共役と共役類を勉強します.類別や同値関係の概念が曖昧な人は,もう一度, 類別 や 整数の加法群の剰余類 , 剰余類 を復習してみてください.
今後,共役をとる操作が非常に大事になります.
共役
集合の二つの元  の間に,次の関係がなりたつとき,
の間に,次の関係がなりたつとき,  を
を  の 共役 (きょうやく)と呼び,
の 共役 (きょうやく)と呼び,  と
と  は共役関係にある,もしくは,互いに共役であるといいます.
は共役関係にある,もしくは,互いに共役であるといいます.

すでに, 群が集合の上で働くということ の記事で,共役の定義は出てきたと思います.しかし,  と
と  を結ぶ関係にも色々あるだろうに,共役という,片一方にだけ
を結ぶ関係にも色々あるだろうに,共役という,片一方にだけ 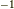 がついた変チクリンな関係にどうして着目するかと感じるかも知れません.共役作用によって,後で勉強する 群の中心 や 正規部分群 という非常に重要な概念が出てくるのです.
がついた変チクリンな関係にどうして着目するかと感じるかも知れません.共役作用によって,後で勉強する 群の中心 や 正規部分群 という非常に重要な概念が出てくるのです.
| [*] | 化学や生化学にも共役という言葉があるようですが,意味は全然違います. |
| [†] | 共役は,昔は共軛と書かれていました.軛は難しい字ですが,訓読みで「くびき」と読みます.馬車で,馬を二頭横につなぐときに使う棒のことです.二つの元が一つのセットとなって働く様子が目に浮かぶような絶妙な訳語でした.しかし,常用漢字外であったので,音だけとって共役と書かれるようになりました.このため,今では意味がよく分からなくなってしまいました.残念なことです. |
| [‡] | 複素数や四元数に共役というのがありました.真ん中の符号を入れ換えて, 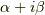 の共役を の共役を  とするものです.これは式(1)とは少し違う操作なので,いまのところ関係ないと思っておいて下さい. とするものです.これは式(1)とは少し違う操作なので,いまのところ関係ないと思っておいて下さい. |
共役の図形的意味
理解の助けの一つとして,いままでに何度も出てきた,図形を回転させる変換では,共役はどのような変換を表わすのかを考えます.
図の  軸回りに,図形を角
軸回りに,図形を角 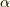 だけ回転させる変換を
だけ回転させる変換を  ,
,  軸回りに角
軸回りに角 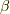 図形を回転させる変換を
図形を回転させる変換を 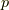 とします.いま,
とします.いま,  の
の 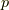 に関する共役元
に関する共役元 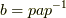 の左作用について,その図形的意味を考えて見ましょう.左作用ですから,
の左作用について,その図形的意味を考えて見ましょう.左作用ですから, 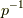 から順番に作用していきます.
から順番に作用していきます.
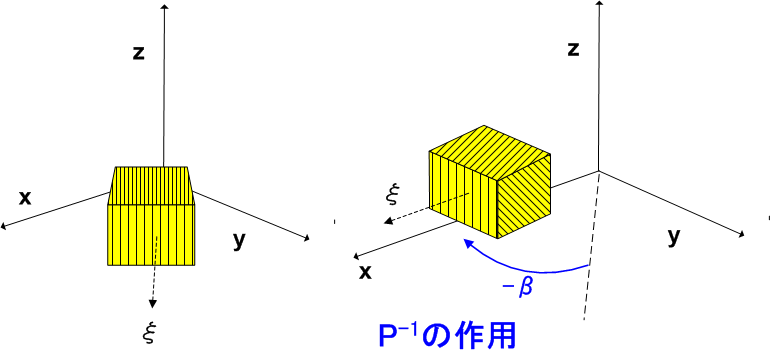
まず 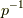 が作用すると,図形は
が作用すると,図形は  軸回りに
軸回りに  だけ回転します.つまり,いままで
だけ回転します.つまり,いままで  平面上で
平面上で  軸と角
軸と角 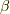 だけずれた方向にあった図形の軸(仮に
だけずれた方向にあった図形の軸(仮に 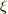 軸と呼びましょう)が,
軸と呼びましょう)が,  軸に一致します.
軸に一致します.

次に  が作用すると,これは定義通り,図形は
が作用すると,これは定義通り,図形は  軸回りに角
軸回りに角 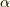 だけ回転します.最後に,
だけ回転します.最後に, 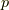 の作用によって図形の
の作用によって図形の 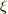 軸はまた元のように,
軸はまた元のように,  軸から角
軸から角 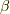 ずれた方向に向きます.
ずれた方向に向きます.
結局, 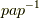 によって図形に対して行われた変換は『
によって図形に対して行われた変換は『 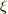 軸回りに,図形を角
軸回りに,図形を角 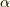 だけ回転させるもの』と同じであったことが分かります.変換
だけ回転させるもの』と同じであったことが分かります.変換  によって行われる回転と同じことが,少しずれた所で,すなわち
によって行われる回転と同じことが,少しずれた所で,すなわち 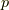 によって表わされる移動分だけずれた所で行われたわけです.
によって表わされる移動分だけずれた所で行われたわけです.
一般に,ある変換  の共役
の共役 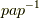 とは『 少しずれた世界で,元の変換aと同様の作用をする変換だ 』と考えられます.そして,その世界のずれを表わすのが
とは『 少しずれた世界で,元の変換aと同様の作用をする変換だ 』と考えられます.そして,その世界のずれを表わすのが 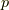 という変換です.
という変換です.
| [§] | 図形の例でない場合, 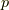 の引き起こす作用がイメージしづらく,『すこしずれた世界』という意味がよく分からないとは思いますが,あまり図形的イメージにばかり頼ってもいられません.いま取り上げた図形の例や,この記事の最後に取り上げる対称群の例を理解の助けに,共役によって『似た働きをする作用』が関係付けられるということを理解できれば,共役に対するイメージとしては十分だと思います.この『似ている』という関連づけが,数学的には,次節で勉強する共役類による類別に他なりません. の引き起こす作用がイメージしづらく,『すこしずれた世界』という意味がよく分からないとは思いますが,あまり図形的イメージにばかり頼ってもいられません.いま取り上げた図形の例や,この記事の最後に取り上げる対称群の例を理解の助けに,共役によって『似た働きをする作用』が関係付けられるということを理解できれば,共役に対するイメージとしては十分だと思います.この『似ている』という関連づけが,数学的には,次節で勉強する共役類による類別に他なりません. |
共役関係による類別
共役がたしかに同値関係であることを確認しましょう.同値関係の定義は,反射律,対称律,推移律の三つを満たすことでした.( 整数の加法群の剰余類 を参照してください.同値関係を忘れてしまった人は, 類別 を復習して下さい.)
- 単位元との共役を取れば
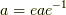 が成り立つので,反射律がなりたちます.
が成り立つので,反射律がなりたちます. - もし
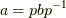 が成り立てば,左側から
が成り立てば,左側から 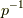 , 右側から
, 右側から 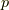 を掛けて,
を掛けて, 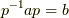 が成り立ちます.
が成り立ちます. 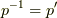 と置けば,これは
と置けば,これは 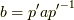 と書き換えられて,対称律になっています.
と書き換えられて,対称律になっています. - もし
 ,
,  が互いに共役ならば,
が互いに共役ならば, 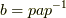 ,
,  を満たす
を満たす 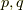 が存在するはずです.このとき,
が存在するはずです.このとき,  となり,推移律もなりたっています.
となり,推移律もなりたっています.
共役は,同値関係だということが分かりましたから,これを使って群を類別することができるはずです.
共役類
群  に対し,ある元
に対し,ある元  に共役な元を全て集めた集合を aの共役類 と呼びます.共役は同値関係でしたから,共役な元を集めることで,群を類別できるのです.基本的には,群を剰余類に分けたときと同じ話なのですが,共役を取ることのイメージが湧きにくい分,剰余類のときよりも難しく感じるかも知れません.いくつか例を見ながら慣れていきましょう.
に共役な元を全て集めた集合を aの共役類 と呼びます.共役は同値関係でしたから,共役な元を集めることで,群を類別できるのです.基本的には,群を剰余類に分けたときと同じ話なのですが,共役を取ることのイメージが湧きにくい分,剰余類のときよりも難しく感じるかも知れません.いくつか例を見ながら慣れていきましょう.
例1
置換 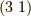 と
と  が共役なことを確認しましょう.
が共役なことを確認しましょう.
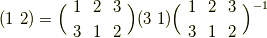
例2
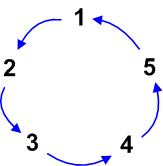
共役の意味が,もう少しはっきりする例として,対称群の元の共役を考えます.5文字の対称群を考えるとき,まず,一つ目のタイプとして  のように,全文の文字が巡回するものがあります.これは,輪になった文字が,グルリと一つずれる様子を想像すると分かりやすいでしょう.
のように,全文の文字が巡回するものがあります.これは,輪になった文字が,グルリと一つずれる様子を想像すると分かりやすいでしょう.
二つ目のタイプとして, 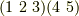 のようなものがあります.これは,図で描けば,二つの巡回サイクルがあって,それらが互いに関係していないような場合です.
のようなものがあります.これは,図で描けば,二つの巡回サイクルがあって,それらが互いに関係していないような場合です.

同様に, 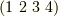 のようなものや,
のようなものや, 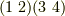 のようなものもあります.
のようなものもあります.
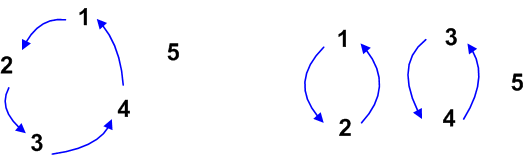
結局,5文字の対称群には,幾つかの文字を不変に保つようなものも含めて,例えば  のようなタイプがあると言えます.
のようなタイプがあると言えます.
例として 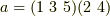 を考え,
を考え,  の共役がどのような元なのかを見てみましょう.一般に5次の対称群は
の共役がどのような元なのかを見てみましょう.一般に5次の対称群は 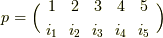 と書けます.これを使って
と書けます.これを使って  の共役
の共役 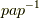 を考えてみましょう.
を考えてみましょう.

ここでは, 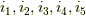 と置いた文字が,個々に
と置いた文字が,個々に 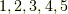 のどれと対応するかは任意ですので,結論として
のどれと対応するかは任意ですので,結論として 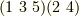 は,一般的に
は,一般的に 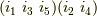 という形をした置換全てと共役であるということが言えます.
という形をした置換全てと共役であるということが言えます.
同様にして, 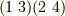 は
は 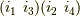 と共役,
と共役, 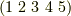 は
は 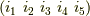 と共役と言えます.結局,対称群に関しては, 共役類による類別が,置換を巡回置換の積として表わすときのタイプ分けになっている ということが言えます.
と共役と言えます.結局,対称群に関しては, 共役類による類別が,置換を巡回置換の積として表わすときのタイプ分けになっている ということが言えます.
群が自分自身に働いていると考えたとき
群  がある集合
がある集合 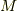 上で働く場合,色々な作用があることは 群が集合の上で働くということ で見ました.ここでは共役作用を考えます.もし
上で働く場合,色々な作用があることは 群が集合の上で働くということ で見ました.ここでは共役作用を考えます.もし 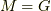 とすると,
とすると,  の元は
の元は  の元自身の共役を取るような働きをすることになり,全ての元の働きを考えると,
の元自身の共役を取るような働きをすることになり,全ての元の働きを考えると,  は共役類で類別されてしまうことになります.さらに,ある元が
は共役類で類別されてしまうことになります.さらに,ある元が  によって移される先を全て集めた集合が軌道でしたが,まさに一つの軌道は一つの共役類になっています. 共役類は,群の共役作用による自分自身の軌道に他なりません .
によって移される先を全て集めた集合が軌道でしたが,まさに一つの軌道は一つの共役類になっています. 共役類は,群の共役作用による自分自身の軌道に他なりません .