この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ボルツマン定数
この記事では,ボルツマン定数の定義である「一分子あたりの気体定数」

(ただし, 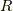 が気体定数で,
が気体定数で, 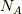 がアボガドロ数)
がアボガドロ数)
と「ボルツマンの関係式」つまり,

( 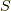 はエントロピー,
はエントロピー,  はある定数,
はある定数, 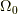 は
系の状態数)
は
系の状態数)
において,

となることを確認します.
理想気体の状態数
まず, 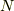 個の単原子分子からなる体積
個の単原子分子からなる体積 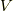 の箱につまっている
理想気体を考えます.
この系の状態数
の箱につまっている
理想気体を考えます.
この系の状態数 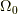 を古典的に求めます.
を古典的に求めます.
この系のエネルギーは,
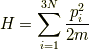
ここで,系の分子のデカルト座標に共役な,
運動量を 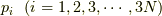 としました.エネルギーが
としました.エネルギーが 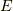 以下の状態数は,
次の式で求められます.
以下の状態数は,
次の式で求められます.
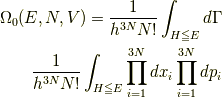
ここで, 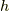 はプランク定数,
はプランク定数, 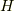 は系の
エネルギー,
は系の
エネルギー, 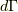 は位相空間における
微小体積要素です.
は位相空間における
微小体積要素です.
位置座標についての積分は, 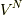 となりますから,
となりますから,
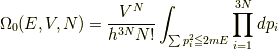
この式の積分部分は,半径 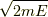 の
の 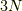 次元の球
の超体積なので [*] ,
次元の球
の超体積なので [*] ,
| [*] | 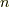 次元の単位球(半径が1の球)の体積
は, 次元の単位球(半径が1の球)の体積
は, 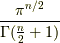 です. です. |
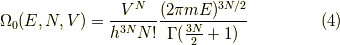
となります.
数学的準備
ここで,ガンマ関数は,
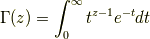
であり,具体的な値としては, 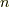 が自然数の時,
が自然数の時,

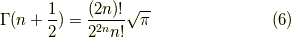
が挙げられます.
また, 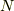 が十分に大きい時成立するスターリングの近似公式
が十分に大きい時成立するスターリングの近似公式
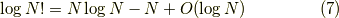
も使います.ちなみに 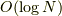 はランダウのオー記号と呼ばれるもので,
カッコ内の式と同程度の小ささであることを示しています.小文字の
はランダウのオー記号と呼ばれるもので,
カッコ内の式と同程度の小ささであることを示しています.小文字の  にすると,
カッコ内の式よりも小さいという事を示します.
にすると,
カッコ内の式よりも小さいという事を示します.
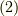 より,
より,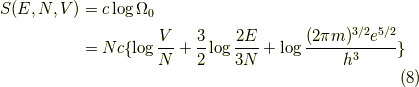
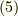 ,式
,式 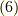 ,式
,式 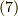 を用いました.
熱力学的関係により
を用いました.
熱力学的関係により 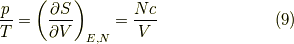
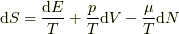 を用います.
を用います.