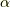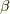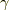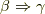この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ハイネ・ボレルの被覆定理と論理学
複素関数論を勉強していて，ハイネ・ボレルの被覆定理というものに出会いました． 詳しくは，「数学・物理解説サイト JSciencer」さんの Heine-Borelの被覆定理 をご覧いただくとして， 論理学的側面から，言いかえを行ってみたいと思います．
定理(下記参考文献からの引用)
その定理というものは次のようなものです．
『z平面上の任意の閉集合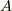 
は，それが開集合 
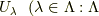は点集合 
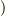の合併集合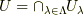 
で覆われているならば，有限個の集合 
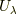で覆われる．』
ここで，
α:z平面上の任意の閉集合 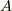である．
β:開集合の合併集合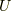 
で覆われている．
γ:有限個の集合で覆われる．
とおくと，この定理の意味するところは，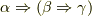 
となります．
この論理を言い換えてみましょう．まず，真理値表を書くと，
| T | T | T | T | T |
| T | T | F | F | F |
| T | F | T | T | T |
| T | F | F | T | T |
| F | T | T | T | T |
| F | T | F | F | T |
| F | F | T | T | T |
| F | F | F | T | T |
となります．
論理的言いかえ
ここで，同値関係にある論理の変形を行います．
その関係とは「対偶法」，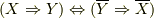 
と，
名前を知りませんが，有名な同値関係（「ならばの否定」とでも言いましょうか．）， 
です
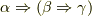． を変形していくと，
一：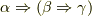
二：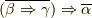 
三：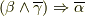 
となります．
さて，「三」のアルファベットに元の意味を代入してみましょう！
（「開集合の合併集合 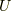で覆われている．」かつ「有限個の集合で覆われない」）ならば「z平面上のある閉集合 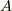ではない．」ということになります．「任意の」は否定すると「ある」に変わるところに注意してください．少し定理の内容が身近になった気がしませんか？
それでは，今日はこの辺で．お疲れ様でした．
