この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ハミルトニアン・ベクトル場
この記事では,正準方程式の座標系に依らない表現の拡張である,
関数  を生成関数とするハミルトニアン・ベクトル場
を生成関数とするハミルトニアン・ベクトル場 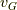 について説明します.
について説明します.
相空間
まず,軽く解析力学の枠組みについて話します.
ラグランジュ形式は配位空間 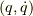 上での物理です.
ハミルトニアン形式は相空間
上での物理です.
ハミルトニアン形式は相空間 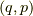 上での物理です.
ラグランジアンが正則な時,この対応は全単射(等価)になります.
これから行う議論は,相空間上の幾何学を扱っていると言う事を,
頭の片隅に置いておいてください.
上での物理です.
ラグランジアンが正則な時,この対応は全単射(等価)になります.
これから行う議論は,相空間上の幾何学を扱っていると言う事を,
頭の片隅に置いておいてください.
正準方程式
正準方程式とは次のハミルトニアンによる運動方程式と等価な方程式のことを言います.
ここで 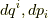 はそれぞれ,
はそれぞれ, 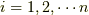 の数だけあるとします.
の数だけあるとします.
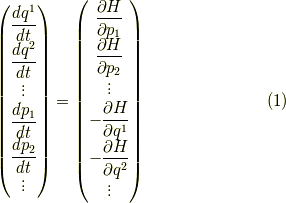
ここで,次を正準2形式 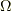 と言います.
と言います.

これはアインシュタインの縮約規則で和をとっています.
微分形式による正準方程式の表現の準備
これを
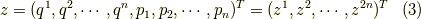
として,列ベクトル  を導入します.
を導入します.
すると,正準2形式(式 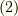 )は次の様に表現できます.
)は次の様に表現できます.
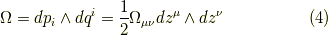
ここで,2階共変テンソル  をn次単位行列
をn次単位行列 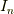 とn次ゼロ行列
とn次ゼロ行列 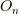 を使って次の様に表します.
を使って次の様に表します.

この逆の2階反変テンソル(逆行列に相当)は,
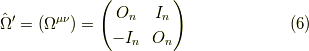
となります.
ここで,正準2形式と二つのベクトルの内積を,
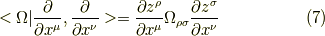
とします.これで準備が終わりました.
正準方程式を微分形式で表す
式 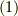 は今までの道具立てで,
は今までの道具立てで,

両辺に 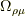 を左からかけて,
を左からかけて,

この式を見て思うことは,左辺が反変ベクトル場,
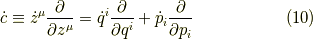
の成分である(取りあえず 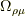 は無視,これを掛けることで一形式になる)のに対して,右辺は一形式
は無視,これを掛けることで一形式になる)のに対して,右辺は一形式
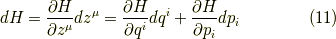
の成分になっています.これらを座標系に依存しない形で表現したいのです.
それを媒介するのが,正準2形式なのです.  で二形式にベクトル場をセットしないことを表せば(結果,縮約相手がおらず二形式は一形式になります.),試しに
で二形式にベクトル場をセットしないことを表せば(結果,縮約相手がおらず二形式は一形式になります.),試しに 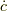 と
と 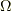 の内積を取ってみます.
の内積を取ってみます.
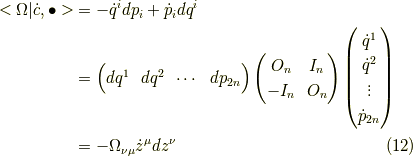
(三行目の添え字が 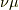 なのにご注意ください.)
すると,一形式になります.一方,正準方程式である式
なのにご注意ください.)
すると,一形式になります.一方,正準方程式である式 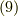 と比較すると,
正準方程式は,
と比較すると,
正準方程式は,

さらに  が反対称テンソルであることからベクトル場のセット位置を変えることで負号が付きます.
が反対称テンソルであることからベクトル場のセット位置を変えることで負号が付きます.

これが正準形式の座標系に依らない表現です.
なお, 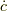 とは,
とは,
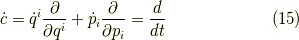
の事です.つまり,ハミルトニアンに共役な量,時間  による微分なわけです.
による微分なわけです.
G(z)を生成関数とするハミルトニアン・ベクトル場
この論理は,ハミルトニアンだけに適用範囲が限られるわけではありません.
ここで,  の滑らかな関数
の滑らかな関数 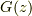 とし,
とし, 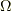 を作用させることで,
を作用させることで,  が
得られるようなベクトル場
が
得られるようなベクトル場 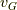 を考えます.
を考えます.
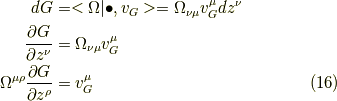
こうして得られるベクトル場 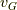
をG(z)を生成関数とするハミルトニアン・ベクトル場と言います.これは物理量にかかることでポアソン括弧を作り出します.
関数  の時は,式
の時は,式  は物理量に作用して微小時間発展(時間パラメータ
は物理量に作用して微小時間発展(時間パラメータ  はハミルトニアンに共役)を表す演算子となり,関数
はハミルトニアンに共役)を表す演算子となり,関数  の様に運動量成分の時は共役な位置
の様に運動量成分の時は共役な位置  の微小並進,関数
の微小並進,関数 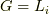 の様に角運動量成分の時は共役な回転角
の様に角運動量成分の時は共役な回転角 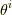 の微小回転に対応するのはご存知の方も多いでしょう.要は,共役な物理量同士の背後には仲立ちをする正準2形式がある訳です.
の微小回転に対応するのはご存知の方も多いでしょう.要は,共役な物理量同士の背後には仲立ちをする正準2形式がある訳です.
つまり,ハミルトニアン・ベクトル場とは,正準方程式の拡張に関する概念であり,ポアソン括弧での微小変換を正準方程式と同じ正準2形式の論理で根拠づける基礎と言えそうです.ポアソン括弧が上位互換としてハミルトニアン・ベクトル場は無視されがちですが,こういう同様に重要な概念には,(ハミルトニアン・ベクトル場という)特別な名前があってもおかしくないですよね.ハミルトニアン・ベクトル場も,こうして得られるポアソン括弧も共にテンソルから作られる量なので,座標系に依存しません.(テンソルの成分自体は座標に依存するのですが,成り立つ物理法則の形(方程式)は座標に依存しません.)
今日はここまで,お疲れさまでした.