この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
双曲線関数の公式１

双曲線関数に成り立つ公式は， 三角関数の公式１ に大変よく似ています．

平方関係

一番目の式は，公式というよりは定義そのものです．

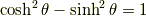
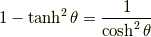
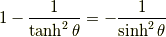
\cosh^2 \theta - \sinh^2 \theta = 1 1-\tanh^2 \theta = \frac{1}{\cosh^2 \theta} 1- \frac{1}{\tanh^2 \theta} =- \frac{1}{\sinh^2 \theta}

加法定理

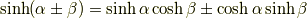
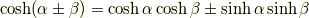
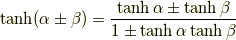
\sinh(\alpha \pm \beta) = \sinh \alpha \cosh \beta \pm \cosh \alpha \sinh \beta \cosh (\alpha \pm \beta) = \cosh \alpha \cosh \beta \pm \sinh \alpha \sinh \beta \tanh (\alpha \pm \beta) = \frac{\tanh \alpha \pm \tanh \beta}{1 \pm \tanh \alpha \tanh \beta}

２倍角の公式

加法定理で 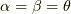\alpha = \beta = \theta と置けば出てきます．

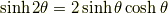
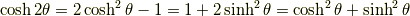
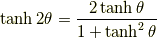
\sinh 2 \theta = 2 \sinh \theta \cosh \theta \cosh 2 \theta = 2 \cosh^2 \theta -1 = 1+ 2\sinh^2 \theta = \cosh^2 \theta + \sinh^2 \theta \tanh 2 \theta = \frac{2 \tanh \theta}{1+ \tanh^2 \theta}

ここで 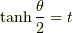\tanh \frac{\theta}{2}=t と置くと，次のようにも表せます．

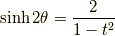
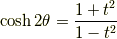
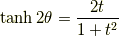
\sinh 2 \theta = \frac{2}{1-t^2} \cosh 2 \theta = \frac{1+t^2}{1-t^2} \tanh 2 \theta = \frac{2t}{1+t^2}

３倍角の公式

加法定理で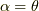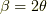， \alpha = \theta , \beta = 2\theta と置き，２倍角の公式を再び使えば導けます．もしくは，オイラーの関係式 \exp ^{\pm \theta} = \cosh \theta \pm \sinh \theta の両辺を３乗して，工夫するのも良い方法です．

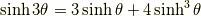
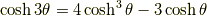
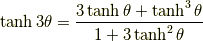
\sinh 3 \theta = 3 \sinh \theta + 4 \sinh^3 \theta \cosh 3 \theta = 4 \cosh^3 \theta -3 \cosh \theta \tanh 3 \theta = \frac{3 \tanh \theta + \tanh^3 \theta}{1+ 3 \tanh^2 \theta}

半角の公式

２倍角の公式から導けます．

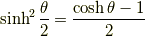
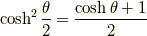
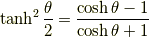
\sinh^2 \frac{ \theta}{2} = \frac{\cosh \theta -1}{2} \cosh^2 \frac{ \theta}{2} = \frac{\cosh \theta + 1}{2} \tanh^2 \frac{ \theta}{2} = \frac{\cosh \theta -1}{\cosh \theta +1}

積和の公式

この公式は，加法定理で 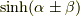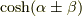\sinh(\alpha \pm \beta) , \cosh(\alpha \pm \beta) を計算しておき，うまく足したり引いたりして導きます．

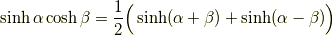
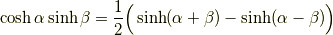
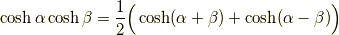
\sinh \alpha \cosh \beta = \frac{1}{2}\Big( \sinh(\alpha + \beta) + \sinh (\alpha - \beta)\Big) \cosh \alpha \sinh \beta = \frac{1}{2}\Big( \sinh(\alpha + \beta) - \sinh (\alpha - \beta)\Big) \cosh \alpha \cosh \beta = \frac{1}{2}\Big( \cosh(\alpha + \beta) + \cosh (\alpha - \beta)\Big) \sinh \alpha \sinh \beta = \frac{1}{2}\Big( \cosh(\alpha + \beta) - \cosh (\alpha - \beta)\Big)

和積の公式

積和の公式で 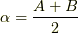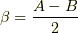\alpha = \frac{A+B}{2} , \beta = \frac{A-B}{2} と置けば導けます．

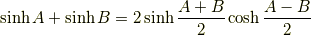
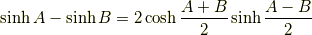
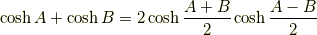
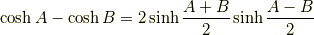
\sinh A +\sinh B = 2 \sinh \frac{A+B}{2}\cosh \frac{A-B}{2} \sinh A -\sinh B = 2 \cosh \frac{A+B}{2}\sinh \frac{A-B}{2} \cosh A +\cosh B = 2 \cosh \frac{A+B}{2}\cosh \frac{A-B}{2} \cosh A -\cosh B = 2 \sinh \frac{A+B}{2}\sinh \frac{A-B}{2}

逆に，和積の公式で 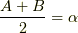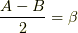\frac{A+B}{2}=\alpha , \frac{A-B}{2}=\beta と置けば積和の公式が得られます．