この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
外積代数
これから,今まで知っていた代数と少し異なる新しい代数を勉強します.代数とは,乗法の定義されたベクトル空間のことでしたが,これから考える乗法は,既にご存知のベクトルの外積に少し似た乗法です.これを 外積代数 と呼びます.しかし,これから考える乗法はベクトルの外積よりも,もっと一般的なものですので,ひとまずベクトルのことは忘れておくと良いと思います.外積代数はそれ自体でも面白いのですが,微分形式もしくは外微分形式と呼ばれる強力なツールを勉強するための土台になります.(微分形式は,物理や工学などに幅広く応用できる強力な理論です.外積代数だけでは,少し数学的すぎて無味乾燥に感じるかも知れません.)どうしても微分形式を早く勉強したい人は,外積代数カテゴリーの後半の記事は飛ばして先に行っても大丈夫ですが,最低 ホッジ作用素 の記事の内容は押さえておいた方が良いと思います.
復習・ベクトルの外積
外積代数を見る前に,三次元ユークリッド空間における,ベクトルの外積を,参考までに復習しておきましょう.
【参考・ベクトルの外積】
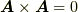
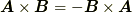 ( 交代則 )
( 交代則 ) (分配則)
(分配則)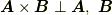
しかし,このような計算は三次元ユークリッド空間以外では,一次元と七次元でしか定義不能でした.( 七次元の外積 参照.)ですから,一般の次元で行うにはあまりにも厳しい計算規則だと言えます.そこで,四番目の規則,すなわち『外積は元のベクトルに直交する』という条件は外してみます.(そもそも直交という概念は内積が定義されていなければ意味がありません.とりあえず,私達は,従来のベクトルから離れたベクトル空間を考えたいのです.)
このように 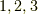 のルールだけに従うことにした,より一般的な計算を, 外積 と呼び,記号は
のルールだけに従うことにした,より一般的な計算を, 外積 と呼び,記号は 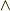 で表わすことにします.名前が
で表わすことにします.名前が  の外積と全く同じだと紛らわしいですので, ウェッジ積 (記号
の外積と全く同じだと紛らわしいですので, ウェッジ積 (記号 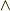 をウェッジと読みます)と呼ぶこともあります.混乱を避けるため,物理のかぎしっぽでは,しばらくはなるべくウェッジ積と呼ぶことにします.(ただし,多くの教科書では外積という呼び名を使っていますので,自習する人は混乱しないようにして下さい.)
をウェッジと読みます)と呼ぶこともあります.混乱を避けるため,物理のかぎしっぽでは,しばらくはなるべくウェッジ積と呼ぶことにします.(ただし,多くの教科書では外積という呼び名を使っていますので,自習する人は混乱しないようにして下さい.)
| [*] | このように,ベクトルの外積の計算を自然に拡張した形でウェッジ積を導入しますが,この先に見えてくる世界は,今まで知っていたベクトルの世界よりもずっと豊潤な内容を含んでいます.楽しみにしていて下さい. |
ウェッジ積の計算
このように定義したウェッジ積がどのような演算規則を満たすかを見てみましょう. 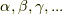 などギリシャ文字はベクトル空間
などギリシャ文字はベクトル空間  の元(つまりベクトル)だとし,
の元(つまりベクトル)だとし, 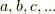 などのアルファベットはスカラー(とりあえず実数)だとします.ベクトルを太字で書くことはやめます.(抽象的な議論が苦手な人は,先に ベクトル空間と線形写像 などを復習してみて下さい.)
などのアルファベットはスカラー(とりあえず実数)だとします.ベクトルを太字で書くことはやめます.(抽象的な議論が苦手な人は,先に ベクトル空間と線形写像 などを復習してみて下さい.)
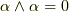 (前セクションのルール
(前セクションのルール 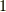 )
)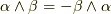 (前セクションのルール
(前セクションのルール 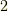 )
)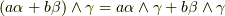 (分配則)
(分配則)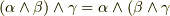 (結合則)
(結合則)
外積代数とは,ベクトル空間  の元が,このようなルールに従って織り成す世界です.『なあんだ,あんまり難しくないなぁ』と思っている人がいるかも知れません.しかし,前セクションの四番目のルールを外してしまった影響をもう少しよく考えてみましょう.
の元が,このようなルールに従って織り成す世界です.『なあんだ,あんまり難しくないなぁ』と思っている人がいるかも知れません.しかし,前セクションの四番目のルールを外してしまった影響をもう少しよく考えてみましょう.
私達がよく知っていたベクトルの外積の計算では,ベクトル  と
と  から作った外積
から作った外積 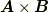 は,向きこそ違う方を向いていましたが,
は,向きこそ違う方を向いていましたが, 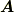 や
や 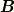 と足したり引いたり出来る同じ種類のベクトルでした.つまり,
と足したり引いたり出来る同じ種類のベクトルでした.つまり, 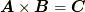 というような計算は,一つのベクトル空間
というような計算は,一つのベクトル空間 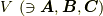 の中で閉じていたわけです.ところが,ウェッジ積では,
の中で閉じていたわけです.ところが,ウェッジ積では, 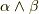 は明からに
は明からに 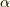 とも
とも 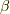 とも違うもので,これ以上簡単化したり分解したりするわけに行きません.そこで,
とも違うもので,これ以上簡単化したり分解したりするわけに行きません.そこで,  に対し,
に対し, 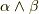 は
は 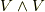 という,
という,  とは異なるベクトル空間に属すると考えます.
とは異なるベクトル空間に属すると考えます.  の外積とウェッジ積との大きな違いは,一つのベクトル空間で演算が閉じていないことのようです.これは少し大変そうですね.
の外積とウェッジ積との大きな違いは,一つのベクトル空間で演算が閉じていないことのようです.これは少し大変そうですね.
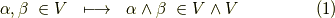
補足ですが,ルール 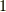 は,ルール
は,ルール  で
で  とおけば,
とおけば, 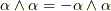 より導けます.ウェッジ積の演算で本質的に特徴的なのは,ルール
より導けます.ウェッジ積の演算で本質的に特徴的なのは,ルール  の 交代性 です.もう一点,注意したいのは,ルール
の 交代性 です.もう一点,注意したいのは,ルール  の結合則です.ベクトルの外積では,一般に
の結合則です.ベクトルの外積では,一般に 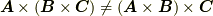 であって,結合則は成り立ちません.これも,いま考えているウェッジ積と,ベクトルの外積の大きな違いです.
であって,結合則は成り立ちません.これも,いま考えているウェッジ積と,ベクトルの外積の大きな違いです.
| [†] | なんだか,ベクトルの外積と違うことが増えてきました.ウェッジ積がどんな演算か分かったら,取り敢えずベクトルのことは忘れましょう.ベクトルの外積から話し始めたのは,その方が初めての人も覚えやすいと思ったからです. |
| [‡] | 実は,ベクトルの外積はウェッジ積から導ける特別な場合なのですが,なぜ同じベクトル空間で演算が閉じていられるのかは, ホッジ作用素 で説明します. |
基底を用いた表現と高次のウェッジ積
いま,  を実数上の
を実数上の  次元のベクトル空間とすると,
次元のベクトル空間とすると,  には独立な基底が
には独立な基底が  個取れます.これを
個取れます.これを 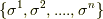 とします.
とします.  の任意の元は,基底を用いて
の任意の元は,基底を用いて 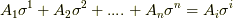 のように基底の一次結合の形で表現できるはずです.(右辺は縮約を使った表現です.)
のように基底の一次結合の形で表現できるはずです.(右辺は縮約を使った表現です.)
さて,  から二階の外積空間
から二階の外積空間 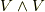 を構成してみましょう.
を構成してみましょう. 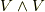 の基底は全て
の基底は全て 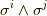 の形をしているはずで,
の形をしているはずで, 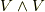 に含まれる任意の元は次の形で表現できると考えられます.
に含まれる任意の元は次の形で表現できると考えられます.

基底には  個の種類があるはずです.
個の種類があるはずです.
| [§] |  個の 個の 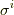 から,二つ選んで から,二つ選んで 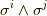 の形を作るからです. の形を作るからです. 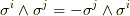 がなりたつため,ウェッジ積の順番が違うだけの基底は独立ではありません.独立な基底は がなりたつため,ウェッジ積の順番が違うだけの基底は独立ではありません.独立な基底は 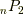 個ではなく, 個ではなく,  個になります.注意しましょう. 個になります.注意しましょう. |
これより, 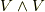 の次元は
の次元は  だと言えます.これは,今後よく使う非常に重要な結果です.
だと言えます.これは,今後よく使う非常に重要な結果です.
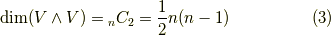
同様に,  の基底は一般に
の基底は一般に  (
(  )と表現され,
)と表現され, 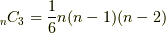 種類あることが言えます.では,このまま外積代数の次元をどんどんあげていくとどうなるでしょうか.(早くも
種類あることが言えます.では,このまま外積代数の次元をどんどんあげていくとどうなるでしょうか.(早くも 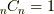 に気づいた人はなかなか勘が良いです.まぁゆっくり考えていきましょう(^_^)/)まず,一般に
に気づいた人はなかなか勘が良いです.まぁゆっくり考えていきましょう(^_^)/)まず,一般に 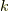 次の外積代数を考えることにします.
次の外積代数を考えることにします. 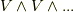 のように書くのは大変なので,これを
のように書くのは大変なので,これを 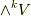 と表記することにします.これを k階の外積空間 と読みます.
と表記することにします.これを k階の外積空間 と読みます. 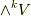 の基底は,
の基底は, 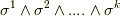 の形に書けるはずですが,
の形に書けるはずですが,  はそもそも
はそもそも  次元で,
次元で, 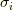 に独立なものは
に独立なものは  個しかありませんでしたから,
個しかありませんでしたから, 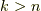 の場合には,
の場合には, 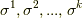 の中に必ず同じものが含まれるはずです.いま,
の中に必ず同じものが含まれるはずです.いま, 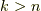 であって
であって 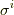 と
と  が同じだとしましょう.
が同じだとしましょう.
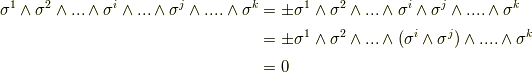
一行目から二行目へは,ウェッジ積のルール 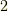 を使って順番に外積の順序を変えて行き,
を使って順番に外積の順序を変えて行き, 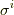 と
と  が隣同士に来るように変形しました.その際,符号は積の順序を何回変えたかによって異なりますが,偶数回か奇数回が分からないので
が隣同士に来るように変形しました.その際,符号は積の順序を何回変えたかによって異なりますが,偶数回か奇数回が分からないので 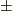 としておきました.(偶数回なら
としておきました.(偶数回なら 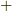 ,奇数回なら
,奇数回なら  です.)三行目では,ウェッジ積の計算に結合則がなりたつことを使い,
です.)三行目では,ウェッジ積の計算に結合則がなりたつことを使い, 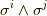 を括弧でくくりました.すると,
を括弧でくくりました.すると, 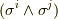 はウェッジ積のルール
はウェッジ積のルール 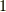 より
より 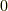 になってしまいます.このように,一般に
になってしまいます.このように,一般に  次元のベクトル空間
次元のベクトル空間  から外積空間を構成する場合,
から外積空間を構成する場合, 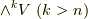 の基底は全て
の基底は全て 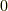 となってしまいます.
となってしまいます.
Important
一般に  を
を  次元のベクトル空間とすると,外積代数の次元は
次元のベクトル空間とすると,外積代数の次元は 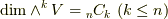 もしくは
もしくは 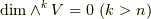 となります.
となります.
ここまでの説明を読んで, テンソル代数 を思い出した人がいると思います.(知らない人は,ここでテンソル代数を勉強しておくことを強くお薦めします.)テンソル代数の枠組みでは,テンソル積という演算により,ベクトル空間  から高階のテンソル空間
から高階のテンソル空間 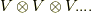 を幾らでも構成することが出来ました.この乗法によってテンソル空間の階数は幾らで上がりますので,『世の中全てのテンソルに関して閉じているベクトル空間』を考えようと思えば,無限次元のテンソル空間までの総和
を幾らでも構成することが出来ました.この乗法によってテンソル空間の階数は幾らで上がりますので,『世の中全てのテンソルに関して閉じているベクトル空間』を考えようと思えば,無限次元のテンソル空間までの総和 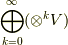 を考えるしかありませんでした.これでは守備範囲をあまりにも広げすぎたという感を否めません.(詳しくは テンソル代数 を参考にして下さい.)
を考えるしかありませんでした.これでは守備範囲をあまりにも広げすぎたという感を否めません.(詳しくは テンソル代数 を参考にして下さい.)
いま考えている外積代数でも,もとのベクトル空間  から
から 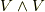 のように,ウェッジ積によって高次のベクトル空間を構成するということでしたが,無限次元にまで拡張する必要はなく,
のように,ウェッジ積によって高次のベクトル空間を構成するということでしたが,無限次元にまで拡張する必要はなく,  の次元までで閉じています.これは著しい違いです.この手頃さが,外積代数がテンソル代数よりもずっと実用的な理由でもあります.
の次元までで閉じています.これは著しい違いです.この手頃さが,外積代数がテンソル代数よりもずっと実用的な理由でもあります.
| [¶] | あとで見るように,実際,外積空間はテンソル空間に『積の交代性』という性質をつけ加えることで作ることが出来ます.テンソル代数の視点からは,外積代数のことを『交代形式のテンソル代数』と見ることが出来ます. |
例えば三次元のベクトル空間では
例えば,三次元のベクトル空間  から外積代数を構成してみましょう.ここまでの内容の復習です.
から外積代数を構成してみましょう.ここまでの内容の復習です.  の基底を
の基底を 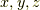 とします.まず,
とします.まず, 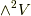 には,
には, 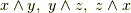 の三つの基底があります.
の三つの基底があります. 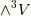 の基底は
の基底は 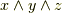 の一つだけです.
の一つだけです.  が三次元なので
が三次元なので  以上は全て
以上は全て 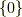 となり,外積代数は
となり,外積代数は 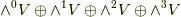 だけで閉じることが分かります.
だけで閉じることが分かります.