無題

物理に悩む人さんの書込 (2006/06/25(Sun) 21:35)

はじめまして，大学生のものです．物理のレポートに関してわからないことがあったため，皆様のお力を貸して頂きたいと思い掲示板を探し，ここに辿り着きました．早速で誠に申し訳ないのですが，問題に対する解法を教えて下さい．天井からバネで吊るされた重り(質量ｍの質点)がある．平衡点を原点として，鉛直上向きにx軸をとる．平衡点からxだけずらすと，大きさkxのバネによる復元力が働き，また速度Vxで動いているとき，大きさrVxの摩擦力が働く．ここで，k及びrは正の定数である．r^2〜0.5mk(左の式の〜は上にもうひとつ〜あり…＝のことかな？)とする． t＝0において，質点を鉛直上方にX0だけ持ち上げてそっと離したときの運動を計算する．という問題です．ご教授お願いします．長文すみません．

Re: 無題

CO さんのレス (2006/06/25(Sun) 22:18)

物理に悩む人さん，こんばんは．

まずは運動方程式をつくり，それを解くという方針で進んでみてください．かかる力は復元力と摩擦力なので，それらを含む式にしてください．

Re: 無題

物理に悩む人さんのレス (2006/06/25(Sun) 22:28)

こんばんは〜早速の返信ありがとうございます．わかりました．早速とりかかってみます．

Re: 無題

物理に悩む人さんのレス (2006/06/25(Sun) 23:06)

この問題に対しての質問です．この問題はまず，自然長を何かに置いて，持ち上げたときにその自然長を超える場合と超えない場合の二種類を考えればいいのですか？もしかして，問題の捉え方を間違ってますか…？

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 00:01)

はじめまして．

> 平衡点を原点として

と書いてあります．このために，元のバネの長さや，その自重，その先の重りの事は，考えなくてもいいのだよといっています．勿論このことは，これらのパラメータが静的には考慮しなくて言いということです．その意味で「原点」と書かれています．

ですから，課題は重りが動的にどのように動くかを運動方程式に書き下すかということです．

Re: 無題

物理に悩む人さんのレス (2006/06/26(Mon) 00:25)

mNejiさんはじめまして，返信ありがとうございます．その平衡点を原点にがいまいちよくわかりません．そういう問題にいままで，触れたことがなかったもので．ネットや教科書を調べても私が求めてる答えが見当たらなくて…(探し方が悪いのだと思われますが…) お手数かけますが，教えて下さいませんか？

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 00:58)

実際に実験をするとして，何が起こりますか？

天井にバネを吊るします．自重で垂れ下がり，例えば25cmとなったとします．
その端に重りをつけます．それによって，5cmのびて30cmとなりました．
そこでしばらく待って，静止させます．これを平衡点とよび，運動の原点とします．

といった感じを「平衡点を原点として」に込めているのだろうと思います．

「原点」が決まれば，1)から2)で出てくる長さなどは一切関係なくなります．

でも，実際の実験をするときには，ある程度「重り」との関係を考慮して，バネの強さや長さを選ばないと，駄目ですね．

バネが強すぎれば，伸びが小さすぎて動かない
摩擦が強すぎて振動解が無い

とか etc が起こります．でも思考上，そんなことは無いように各種パラメータは与えてあるものと仮定せよ，と言うことです．

従って； >この問題はまず，自然長を何かに置いて，持ち上げたときにその自然長を超える場合と超えない場合の二種類を考えればいいのですか？

これは杞憂となりますね．

Re: 無題

物理に悩む人さんのレス (2006/06/26(Mon) 01:20)

夜遅くに，こんなに丁寧に書いてもらってすみません．おかげで理解することができました．また質問等がでてきましたら，今日の夜にまた書き込みをしますので，そのときはまたよろしくお願いします．

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 04:01)

もう寝ますのでヒントだけ

時間: 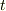x方向の加速度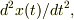： d^2 x(t)/dt^2 , x方向の復元力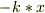： -k*x x方向の摩擦力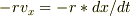： -rv_x = -r*dx/dt

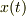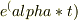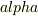運動の方程式を立てると， x(t) は，時間について2次で強制力のない微分方程式．視察により， e^(alpha*t) を仮定し， alpha の2次方程式を得る．この解の判別別けに従って，一般解を得，初期条件をいれて完成．

微分方程式の解法は数学の問題で，とく時間がないので悪しからず．

Re: 無題

物理に悩む人さんのレス (2006/06/26(Mon) 16:45)

mNejiさんヒントありがとうございます．一応，答えらしきものがでてきたのですが…合ってるかどうかが不安です．最終的にグラフを書くため，x(t)＝の式を書きます．X(t)＝−r^2x0t＋kx(rt−m＋me^−rt/m)/r^2+x0になりました．

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 20:02)

いま拝見しましたが，残念な事に解は違うように思います．

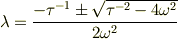
$\lambda = \frac{-\tau^{-1} \pm \sqrt{ \tau^{-2} - 4\omega^2}}{2\omega^2}$

きっとインターネットには，2階の線形微分方程式の解法のサイトがあるので，それを見てください．その内，理解しやすいサイトがあれば，ここに書き込んでくださいませんか？

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 22:36)

途中まで書いたのを，操作ミスで消してしまいました．簡単にレビューします．

運動方程式：

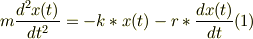
$m\frac{d^2 x(t)}{dt^2} = -k*x(t) -r*\frac{d x(t)}{dt} (1)$

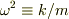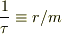ここで, 定数を定義； $\omega^2 \equiv k/m$ (2) $\frac{1}{\tau} \equiv r/m$ (3)

運動方程式を整理すると

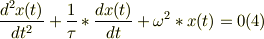
$\frac{d^2 x(t)}{dt^2} + \frac{1}{\tau}*\frac{d x(t)}{dt} +\omega^2*x(t) =0 (4)$

与式は時間について2階の線形同時方程式だから,その特解として

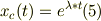
$x_c(t) = e^{\lambda*t} (5)$

ここで $\lambda$ は定数で，以下で求める．

(5)を(1)に代入して整理すれば，

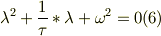
$\lambda^2 + \frac{1}{\tau}*\lambda +\omega^2 =0 (6)$

これを解けば

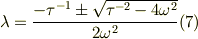
$\lambda = \frac{-\tau^{-1} \pm \sqrt{ \tau^{-2} - 4\omega^2}}{2\omega^2} (7)$

根号の中身 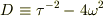$D \equiv \tau^{-2} - 4\omega^2$ によって場合別けする .

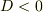の時

まだ途中．．．

Re: 無題

物理に悩む人さんのレス (2006/06/26(Mon) 22:48)

レビューありがとうございます．そうでしたか… なるほど…わかりました．2階の線形微分方程式の解法のサイトをちょっと探してきます．最終的な答えは，No.9993のようになればいいのですか？

Re: 無題

mNeji さんのレス (2006/06/26(Mon) 23:06)

>最終的な答えは，No.9993のようになればいいのですか？

まだ先が続きます．こちらのTeX記法になれていなくて，書くのに時間が掛かります．

恐らく，私が書き上げるよりも，インターネットで見られる方が速いかとおもいます．私は，練習と思って書いてみます(汗)．

Re: 無題

物理に悩む人さんのレス (2006/06/26(Mon) 23:12)

お手数かけて本当にすみません〜ｍ(＿＿)ｍよろしくお願いします．私も一応探ってみます．

Re: 無題

mNeji さんのレス (2006/06/27(Tue) 00:16)

こちらのサイトのTeXには，まだ当分慣れないようなので，自分のサイトで式をけんとうします．

ところで，質問のところに

> r^2〜0.5mk(左の式の〜は上にもうひとつ〜あり…＝のことかな？)とする．

これは 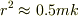$r^2 \approx 0.5mk$ 見たいでしたか？

> t＝0において，質点を鉛直上方にX0だけ持ち上げてそっと離したときの運動を計算する．という問題です．

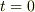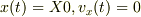これは，初期条件 t=0 に於いて x(t)=X0, v_x (t)= 0 として解釈しますね．

Re: 無題

物理に悩む人さんのレス (2006/06/27(Tue) 00:49)

はい，それです！

Re: 無題

mNeji さんのレス (2006/06/27(Tue) 04:00)

とりあえず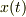， x(t) の一般解を求めました．検算してません．

残念なことに，こちらのサイトのフォーマットに変換する時間が無いので，

mNjB:dynamics/spring_with_friction

http://www.as-ia.co.jp/ykwk/wiki.cgi?dynamics%2fspring_with_friction

を見てください．

Re: 無題

物理に悩む人さんのレス (2006/06/27(Tue) 05:04)

こんな夜遅くまでやってもらちゃって本当に申し訳ないです．解まで求めてもらってしまって… ここまでやってもらって誠に申し上げにくいのですが，式が解読できませんでした．(ああいう式は初めてみたもので…) 流れがわかったのでこれから少しやってみようかと思います．こんな私に付き添って頂き感謝しております．また，なにかありましたら何とぞよろしくお願いします．

Re: 無題

toorisugari no Hiro さんのレス (2006/06/27(Tue) 16:03)

mNejiさま余計なお世話かもしれませんが，#9995でTeXがうまく変換しなかったのは2Byteコード(「全角」の空白)を使われているためです．これを直されたらうまくいきますよ．

Re: 無題

mNeji さんのレス (2006/06/27(Tue) 19:18)

>#9995でTeXがうまく変換しなかったのは2Byteコード(「全角」の空白)を使われているためです．

ご指導，ありがとうございます．昨晩は，極度に混乱してしまいました．;P

もし宜しければ，疑問があります；

式番号をつける環境はありますか？もし無い場合，式と式番号を離す手法は？
判別式の場合別けの左・波括弧はどうすればよいですか？
分数形式の簡易表示法はありますか？
典型的な使用例のサイトはありますか？

お教えくだされば，幸いです．「LaTeX落ちこぼれ」より．

Re: 無題

toorisugari no Hiro さんのレス (2006/06/27(Tue) 19:35)

TeXというよりこのサイトに特化したものですから，私より管理者の方が適任でしょうが，，，

>1) 式番号をつける環境はありますか？もし無い場合，式と式番号を離す手法は？

私はquad,qquadでスペースあけるしか知りません．

>2) 判別式の場合別けの左・波括弧はどうすればよいですか？

caseに相当する機能はないような気がします．

>3) 分数形式の簡易表示法はありますか？

?? frac以外に分数の表示法はあるか?ということなら，ないのでは?

>4) 典型的な使用例のサイトはありますか？

ないと思います．

Re: 無題

mNeji さんのレス (2006/06/27(Tue) 20:03)

>私はquad,qquadでスペースあけるしか知りません．

判りました，感謝します．

Re: 無題

CO さんのレス (2006/06/27(Tue) 20:37)

>1) 式番号をつける環境はありますか？もし無い場合，式と式番号を離す手法は？

tag{1} というように，tagコマンドを用います．

$F = ma \tag{1}$

自動で数式番号を振ることはしていません．

Re: 無題

Chappy さんのレス (2006/06/27(Tue) 21:01)

mNejiさん，こんなのはどうでしょうか？？

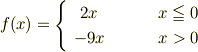
$f(x)=\left\{\begin{array}{c@{\hskip 16mm}c}2x & x\leqq 0 \\-9x & x> 0 \\\end{array}\right.$

f(x)= left{ begin{array}{cc} 2x & xleqq 0 \ -9x & x> 0 \ end{array} right.

僕はいつもcaseは使いません．left〜right.が好みです．このコマンド(?)はかなり便利です．

Re: 無題

toorisugari no Hiro さんのレス (2006/06/27(Tue) 21:13)

array環境を＜tex＞＜/tex＞の中で使えるのですね．知らなかった． (使えるのはarray環境だけですか? > 管理者様) これは便利なものを教えてもらいました．ありがとうございます．

Re: 無題

Chappy さんのレス (2006/06/27(Tue) 21:16)

お役に立てたのなら，嬉しいです．．

僕もbegin環境が使えることを知ったのが収穫です．つくづく，この掲示板はすごいなと思います． LaTeXが環境が整っているのは便利ですね．

Re: 無題

CO さんのレス (2006/06/27(Tue) 23:43)

> 使えるのはarray環境だけですか? > 管理者様

align環境の中で使えるものは全て使えるはずです :-)

Re: 無題

mNeji さんのレス (2006/06/28(Wed) 00:13)

皆様，Tipsのご教授ありがとうございました．

COさん： tag{88} は便利ですね．利用させていただきます．

そういえば，日本語が通らないということは，mimeTexベースとか？

Chappyさん： begin{array}{cc}云々... は，難しいですが，コピーして使わせていただきます．

なお，{cc}は何のおまじないですか？取ったり，{bb}などやりましたが全滅．

また，「right.」の後ろのピリオッドは？

お陰さまで，簡単な表現には困らないようになったと思います．ペコリ．

Re: 無題

toorisugari no Hiro さんのレス (2006/06/28(Wed) 00:39)

> なお，{cc}は何のおまじないですか？ {}の中身は配置を指定する引数で，おまじないではないです．要素の個数だけ必要です．

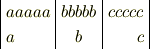
$\begin{array}{|l | c | r|}aaaaa & bbbbb & ccccc\\a & b & c\end{array}$

begin{array}{|l | c | r|} aaaaa & bbbbb & ccccc\ a & b & c end{array} のように2段目が左揃え，中そろえ，右揃えになっています． right.はなにも出力しないときにつかいます．right}に置き換えてみてください．

Re: 無題

mNeji さんのレス (2006/06/28(Wed) 02:25)

toorisugari no Hiroさん：

詳しいご説明，ありがとうございました．これで，私レベルの数式はほぼ書ける様に思います．:D

追伸:

先ほど，隙間時間ができたので，冷静にテストしました．だいぶ判りました．感謝にたえません．

そして，LaTeXコマンドシート一覧

http://www002.upp.so-net.ne.jp/latex/

を再度眺めました．これは，前回，数式を書こうとして混乱した時にも拝見したのですが，その時にブラウズしようとして巧く出来なかったので，そのままにしていました．

自分の癖で，目次の項目にマウスをもってくる(ホバーする)と，その項目に色がついたり，アンダー・ラインがつく等の視覚的変化を期待します．

例示すると

1.はじめに

1.1 このページについて

私の感触では，「1.はじめに」の何処にマウスをホバーしても，そこがアクティブとなると思いました．そころがクリックしても何も変化が無かったので，諦めたしだいです．

先ほどの経験では，サブ・セクションの項目名「このページについて」にホバーしてクリックすればジャンプできるのに気が付きました．

ずいぶんとお馬鹿なユーザの為に，皆様にお手数をお掛けしたことをお詫びもうしあげます．

ついては，この本題である「微分方程式の解」を出す文章を「LaTeXコマンドシート一覧」に従って，書いてみようと思います．

Re: 無題

CO さんのレス (2006/06/28(Wed) 12:10)

> mNeji さん > そういえば，日本語が通らないということは，mimeTexベースとか？

これは「通らない」ではなくて「通さない」ようにしています．

Re: 無題

mNeji さんのレス (2006/06/29(Thu) 03:22)

COさん：

>これは「通らない」ではなくて「通さない」ようにしています．

了解いたしました．ご教示感謝いたします．

Re: 無題

mNeji さんのレス (2006/07/01(Sat) 14:35)

以前,回答をこちらの数式表現に改めるようなことを言いましたが，まだ出来ていません．

他方，微分法的式の解法はインターネットに一杯あると予想したものの，ほんとあるかどうか判らなかったので，

yahooで[常微分線形方程式 2階]を検索してみました．そのトップに下記のサイトがありました．ざっと拝見しましたが，とても確りした誤説明だとおもいました．

・線形常微分方程式 http://www.geocities.jp/ruy406/math/math8.pdf#search= '%E5%B8%B8%E5%BE%AE%E5%88%86%20%E7%B7%9A%E5%BD%A2%E6%96%B9%E7%A8%8B%E5%BC%8F%202%E9%9A%8E'

少なくとも，古典力学の典型問題として，上記の解法をじっくり身につけていれば，応用も利くと思います．

今回は触れませんでしたが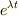， $e^{\lambda t}$ の関数を仮定するのは，数学の便法以上の物理学的意味があると感じています．

独立な $\lambda$ で一般解を展開するというのは，量子力学で固有値問題をといて，固有値ベクトルで波動関数を展開するのとは，ある意味で同形の問題です．

また $\lambda$ が同根のばあい，縮退を解く，という考え方も，量子力学でも類推できますね．

また，指数関数と複素数関数を同等に計算しておくと，三角関数の面倒な計算から開放される醍醐味が身につきます．その中でも，初期条件からパラメータを決めていく一連の作業で， 1) 定数係数が複素共役となっているか 2) 最終結果で，きれいに虚数部が消えているか

という，検算がやれるのは，三角関数表記の計算では不可能な特徴です．

以上，老人の呟きでした．

[home] [掲示板] [ページの先頭]