代数の問題について
代数の問題について
Chappy さんの書込 (2006/06/24(Sat) 18:53)
たびたび失礼します,大学生のChappyです.
今,僕の手元に,ある問題があって,
よいアドバイスがいただきたく,質問いたします.
その問題は
<b>“ 有限整域  は体であることを示せ ”</b>
というものです.
ただし,
は体であることを示せ ”</b>
というものです.
ただし,  は単位元をもつという仮定が必要かもしれません.
は単位元をもつという仮定が必要かもしれません.
 は自明なイデアルしかもたないと僕は考えてます.
もし,それが正しければ,
単項イデアル
は自明なイデアルしかもたないと僕は考えてます.
もし,それが正しければ,
単項イデアル 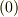 が極大イデアルとなるため,
“
が極大イデアルとなるため,
“  :極大イデアル
:極大イデアル 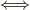
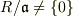 :体 (
:体 (  は環)”という事実を用いれば,証明できると考えています.
いかがでしょうか?
また,違うアプローチがあれば,ヒントだけ教えていただけると嬉しいです.
は環)”という事実を用いれば,証明できると考えています.
いかがでしょうか?
また,違うアプローチがあれば,ヒントだけ教えていただけると嬉しいです.
Re: 代数の問題について
Chappy さんのレス (2006/07/05(Wed) 23:36)
その後,自力で解けました.
自分で考えた予想が正しかったようです...
むしろ,自明なイデアルしかないことから,簡単に  が体であることが言えました.
が体であることが言えました.
話は変わりますが,1つ質問です.
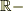 係数の形式的べき級数環
係数の形式的べき級数環
![\mathbb{R}[[x]]=\{a_0+a_1x+a_2x^2+\cdots\:|\:a_i\in\mathbb{R}\}](http://hooktail.maxwell.jp/bbslog/d455d8e995787144a3cf3177bd37d1b8.png) の単数全体はどうして,
の単数全体はどうして,
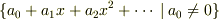 となるのですか?
となるのですか?
Re: 代数の問題について
mNeji さんのレス (2006/07/06(Thu) 01:39)
Chappyさん:
なんどか,解説されているところを拝見させていただいています.
このような数学の問題は,記号を見ただけで眠たくなる習性の持ち主です(泣).そこで,Chappyさんの質問も勿論理解できないのですが,将来,この問題を知りたい人も出ると思います.ついては,折角解かれた解法をお書きになると良いのではありませんか?
ヒョットすると数学に堪能な方から,コメントをいただけるかも知れませんから.
Re: 代数の問題について
Chappy さんのレス (2006/07/06(Thu) 18:08)
mNejiさん,ご返事ありがとうございます! そうですか..それでは,解答を書いてみます...
<b><有限整域  が自明なイデアルしかもたないこと></b>
が自明なイデアルしかもたないこと></b>
証明の方針は背理法で,自明でないイデアル 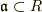 があったと仮定するところから始めます.
があったと仮定するところから始めます.
 は自明でないから,ある0でない元
は自明でないから,ある0でない元 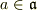 があります.
よって,イデアルの定義から,
があります.
よって,イデアルの定義から, 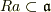 が成り立ちます.
が成り立ちます.
 は有限だから,
は有限だから, 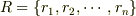 などと書けます.
すると,
などと書けます.
すると,  が整域であることを使えば,
が整域であることを使えば,
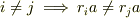 であることが分かります.したがって,位数を比べると,
であることが分かります.したがって,位数を比べると,
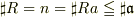 .
.
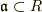 であることから,
であることから, 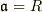 となり,
となり,
 が自明なイデアルでないことに矛盾します.
が自明なイデアルでないことに矛盾します.
<b><  が自明なイデアルしかもたないならば,
が自明なイデアルしかもたないならば,  が体であること></b>
が体であること></b>
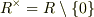 であることを示します.
背理法で,0でない元
であることを示します.
背理法で,0でない元 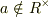 が存在したとします.
このとき,
が存在したとします.
このとき, 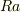 は
は  のイデアルです.
ところが,
のイデアルです.
ところが,  には自明なイデアルしかないので,
には自明なイデアルしかないので,
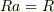 です.したがって,ある
です.したがって,ある 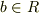 があって,
があって, 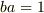 .
同様に
.
同様に 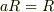 から,ある
から,ある 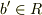 があって,
があって, 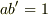 .
実は,
.
実は,
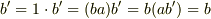 となりますから,
となりますから, 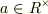 となり,矛盾がおきます.
となり,矛盾がおきます.
質問の補足ですが,
![\mathbb{R}[[x]]](http://hooktail.maxwell.jp/bbslog/d9c9650f2d288ad8f2cfbb19cc9197aa.png) には次の乗法が定義されているものとします.
には次の乗法が定義されているものとします.