単振り子の直交座標の微分方程式
単振り子の直交座標の微分方程式
りきがー さんの書込 (2006/06/22(Thu) 19:34)
はじめまして,大学生なんですが,単振り子の微分方程式をたてるときって,普通は自然座標系か二次元極座標系を使いますよね?そこで,質問なんですけど,単振り子を直交座標成分にわけて,微分方程式を解くことって可能なのでしょうか?可能ならば,どうやれば,速度v(dx/dt)や変位xを求めることができますか?
単振り子の式
mA↑=mg↑+T↑(張力)
これを直交座標成分に分解すると,
x成分
m(Ax)=Tsinα
y成分
m(Ay)=mg-Tcosα
ここから微分方程式を使えば速度Vのx,y成分を求めることができるらしいのですが,微分方程式の解き方がわかりません.どのようにといたらいいでしょうか?
Re: 単振り子の直交座標の微分方程式
toorisugari no Hiro さんのレス (2006/06/22(Thu) 20:39)
不可能ではないですが相当ややこしいかな? まず,完全な微分方程式を得なければいけません.(これだけでも結構勉強になるような..)
そのためには, 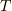 が未定なのでこれを決定しなければいけませんが,それには,拘束条件「糸の長さは変わらない」を考慮しなければいけません.
が未定なのでこれを決定しなければいけませんが,それには,拘束条件「糸の長さは変わらない」を考慮しなければいけません.
軸座標系なら自然に導入できますが,直角座標系なら
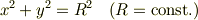
を使って 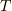 を消去しなければいけません.なお,この式をそのまま使うより,
を消去しなければいけません.なお,この式をそのまま使うより,  で複数回微分して考えた方がよいと思います.(高校なら遠心力も含めた釣り合いで考えるのでしょうが,ここはがんばって計算してください.)
で複数回微分して考えた方がよいと思います.(高校なら遠心力も含めた釣り合いで考えるのでしょうが,ここはがんばって計算してください.)
とりあえず,こうして 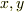 の完全な微分方程式が得られますが,それを解くのは...かなり無理かと...(軸座標系に戻すしかないような)
の完全な微分方程式が得られますが,それを解くのは...かなり無理かと...(軸座標系に戻すしかないような)
Re: 単振り子の直交座標の微分方程式
りきがー さんのレス (2006/06/22(Thu) 21:52)
早速のレスありがとうございます.
せめて張力Tが変位(x)や速度(v)の関数で表せたらとけるんですが...
const.って何ですか?すみません,無知なもので...まだ数学では微分方程式はおそわってないですね...物理の授業でさわりをやっただけです.なのに教授は,「単振り子の直交座標の微分方程式をたてて,それぞれの成分についてのvを求めるように」といってきました汗
Re: 単振り子の直交座標の微分方程式
toorisugari no Hiro さんのレス (2006/06/22(Thu) 22:09)
> せめて張力Tが変位(x)や速度(v)の関数で表せたら
できますよ.上の考えをよく理解してください.
> const.って何ですか?
constantの略.(後は辞書を見てください.)
> 微分方程式はおそわってないですね
微分を知っていれば方程式を出すまではいけます.がんばってください.
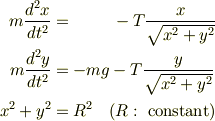
これから2階微分の項を消去すればいいのです.
> それぞれの成分についてのvを求めるように
これは無理っぽいような...角運動量の方程式を求めるならまだしも...
Re: 単振り子の直交座標の微分方程式
mNeji さんのレス (2006/06/22(Thu) 22:34)
水泳の腕や脚の計算をしようと準備中です.これに近い話が幾つか派生するのでちょっと気になっていますが...
この手の糸の問題は;
+糸が伸び縮みしない +糸が撓みもしない
というのがとても重要です.まるで質量のない剛体リンクと同じです.
ですから「toorisugari no Hiro」さんが提示されたように,xy座標系で考えると「T」と前面対決という不毛の戦いに巻き込まれると思います.
やはり極座標の土俵の基,
+回転角度の接線成分の運動方程式を解いて, +必要なら,動径方向の運動方程式より,「T」を計算する
のが筋では? 連立微分方程式を数値積分で解くのは,それこそ多関節リンクのような場合ではないでしょうか?
Re: 単振り子の直交座標の微分方程式
mNeji さんのレス (2006/06/22(Thu) 22:41)
追伸
やや生意気にいえば,Tが決まるから運動が決まるわけではない.運動が解けるから,Tが決まるのだとおもいます.
確かに,高校生のころ,幾つもの仮説がでてから「振り子の動き」が出されたので,とても抵抗を感じたような記憶が,ほんのりと思い出しました(笑).
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/23(Fri) 00:41)
toorisugari no Hiro さんの書かれた最初の方程式にdx/dt,2番目の式にdy/dt を掛けて足し合わせてから 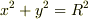 を利用すると,T が消去されて,それを積分すると次のエネルギーの積分が得られます.
を利用すると,T が消去されて,それを積分すると次のエネルギーの積分が得られます.
![\frac{1}{2}m\left[\left(\frac{dx}{dt}\right) ^2+\left(\frac{dy}{dt}\right) ^2\right] +mgy=E](http://hooktail.maxwell.jp/bbslog/6332277a8370bf3171fea5707c03bcbe.png) (これはエネルギーの保存を表す式なので,運動方程式を用いなくても書くことができるでしょう.)
一方,
(これはエネルギーの保存を表す式なので,運動方程式を用いなくても書くことができるでしょう.)
一方, 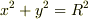 より
より 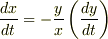 となり,従って
となり,従って 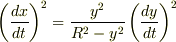 が得られます.
この関係を用いるとエネルギーの積分は
が得られます.
この関係を用いるとエネルギーの積分は
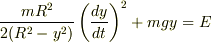 となるので,これから速度のy成分
となるので,これから速度のy成分 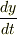 を
を  だけの式で表すことができます.
その結果,変数分離型の微分方程式が得られ,積分して解くことができますが,積分の実際の計算は相当面倒なものになりそうです.
だけの式で表すことができます.
その結果,変数分離型の微分方程式が得られ,積分して解くことができますが,積分の実際の計算は相当面倒なものになりそうです.
Re: 単振り子の直交座標の微分方程式
なんとなく さんのレス (2006/06/23(Fri) 01:20)
こんにちは.
yamaさんのやりかた(第一積分)で,(x,y)方向の速度は求まりましたが,これ,単振り子ですよね.ということは,すでにエネルギー積分の式にも片鱗が現れていますが,位置(x,y)そのものは,けっきょくは楕円積分となり,解析解はそこどまりのはずですね. 初等教育問題としては,少し不適切な気もします.
Re: 単振り子の直交座標の微分方程式
toorisugari no Hiro さんのレス (2006/06/23(Fri) 09:58)
> これから速度のy成分 frac{dy}{dt} を y だけの式で表すことができます.
おお,すごい.
前言の > これは無理っぽいような... は撤回させていただきます.
Re: 単振り子の直交座標の微分方程式
トンガリ さんのレス (2006/06/23(Fri) 10:38)
x=sin ωtを微分してx’=ω cos ωtさらに微分して x’’=−ω^2 sin ωt =−ω^2 x・・・・・? は高校で習ったが,微分方程式の解き方を習ってないのが,このテーマの特徴である.
y軸を鉛直下向きに置いたx-y直角座標系で,糸の長さR,糸とy軸の成す角をθとして, θ=0 から重りを水平方向に少しのAだけ変位させてから,そっと離した場合を考えると, 近似的に糸の張力 = 重りの重力 近似的に水平方向の復元力 = 糸の張力 sin θ = 重りの重力 x/R
よって,水平方向の運動方程式は 近似式mx’’=−mg x/R整理してx’’=−g/R x
ここでω^2=g/Rとおくと, 近似式x’’=−ω^2 x・・・・・・・・・・・・・・・・?
?と?の右辺を比較すると同じ式だ.あえて?を積分しなくても,解は ?の微分前の式だ. これを大学らしく表現すると, x=A sin (ωt+θ.)が?の一般解だ.半振幅A と 位相θ.を 任意定数と呼ぶが,初期条件A で離した時からの時間を tとすると,θ. が 90°と決まる.
重要なのは振動の周期であって,ω^2=g/Rから,周期の近似式2π√(R/g)を得た. 鉛直方向の運動方程式は,水平方向の解が求まった今は無用である.
ちなみに,振り子の振動とは違って,近似の必要のない最も単純な, バネ定数Kの先に質量mが付いた振動ではω^2=K/mから,周期2π√(m/K)を得る. 『 バネ秤は単振動.その復元力は変位に比例するわな! 』と憶えておくこと.
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/24(Sat) 09:24)
微分方程式を用いると難しくなってしまいましたが,「速度成分をそれぞれの座標の関数として表す」ということに限れば,微分方程式を用いなくても,高校物理の範囲で解答できます.
エネルギーの保存の式 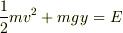 を用いると,速さ
を用いると,速さ  を
を  だけの式で表すことができます.
その式で
だけの式で表すことができます.
その式で 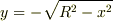 と置くと,
と置くと,  を
を  だけの式で表すことができます.
速度成分は,
だけの式で表すことができます.
速度成分は, 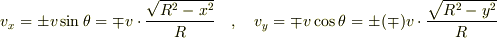 となります.
ただし,
となります.
ただし, 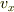 の式では
の式では  が
が  だけの式で,
だけの式で, 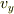 の式では
の式では  が
が  だけの式で表されているものとします.
(初めに書いた式に誤りがあったので修正しました.)
だけの式で表されているものとします.
(初めに書いた式に誤りがあったので修正しました.)
Re: 単振り子の直交座標の微分方程式
りきがー さんのレス (2006/06/24(Sat) 22:49)
皆さん,ありがとうございます!!
ところで,toorisugari no HiroがたてたY成分の式のmgって,どうしてマイナスになるんでしょうか?g↑の成分が(0,-g)だからですか?
あと,yamaさんが教えてくださった
>>toorisugari no Hiro さんの書かれた最初の方程式にdx/dt,2番目の式にdy/dt を掛けて足し合わせてから を利用すると,T が消去されて,それを積分すると次のエネルギーの積分が得られます.
のdx/dtとdy/dtをかけるというところで質問があるんですが,それは式の両辺にそのまんまかけたらいいんですか?
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/25(Sun) 00:10)
>ところで,toorisugari no HiroがたてたY成分の式のmgって,どうしてマイナスになるんでしょうか?g↑の成分が(0,-g)だからですか?
その通りです.つまり,上向きにy軸をとっているからです.なお,支点を原点にとっているので最下点の座標は(0,-R)になります.
>のdx/dtとdy/dtをかけるというところで質問があるんですが,それは式の両辺にそのまんまかけたらいいんですか?
その通りです.
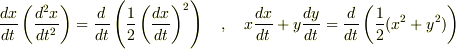 のような関係が成り立つことに注意しましょう.
のような関係が成り立つことに注意しましょう.
Re: 単振り子の直交座標の微分方程式
りきがー さんのレス (2006/06/25(Sun) 09:53)
ありがとうございます.
実際に演算を行っているのですが,Tの消去の方法がわかりません.X^2+Y^2=R^2でどのように使えばTを消去することができるのでしょうか?
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/25(Sun) 10:32)
R^2 は定数なので,微分すれば0になります.
Re: 単振り子の直交座標の微分方程式
りきがー さんのレス (2006/06/25(Sun) 16:43)
>>R^2 は定数なので,微分すれば0になります.
それはわかるんですが,その式をどう使ってTを消せばいいのかがわかりません...
足し合わせてもTが残ってしまっています.Tを他の文字で表してたらいいんでしょうか?
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/25(Sun) 18:08)
T を含む項だけを計算すると次のようになります.
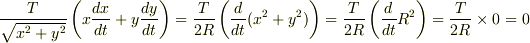
Re: 単振り子の直交座標の微分方程式
yama さんのレス (2006/06/26(Mon) 00:00)
理解できたようで良かったですね.
ただ計算したら T が消えたというだけでなく,その背後にある物理的な意味も理解しておいてほしいと思います.
No.9975の計算は, 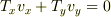 であることを示したものです.
これはベクトルの内積を用いると
であることを示したものです.
これはベクトルの内積を用いると 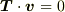 ということですが,張力
ということですが,張力 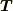 と速度
と速度  が互いに垂直であることを考えると,この関係は当然のことですね.
また,
が互いに垂直であることを考えると,この関係は当然のことですね.
また, 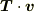 は張力
は張力 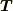 の仕事率ですが,「張力は運動方向に垂直にはたらくので仕事をしない」ということからも,この仕事率が0になることが分かるでしょう.
このように,張力や垂直抗力が仕事をしない場合は,それらの力はエネルギー保存の式には現れないことが分かると思います.
の仕事率ですが,「張力は運動方向に垂直にはたらくので仕事をしない」ということからも,この仕事率が0になることが分かるでしょう.
このように,張力や垂直抗力が仕事をしない場合は,それらの力はエネルギー保存の式には現れないことが分かると思います.